Компетентность и экономическая эффективность

Компетентность и экономическая эффективность

Рассмотрим теперь превращение компетентностей в экономический результат. Проводя дальше линию анализа экономики как решения задач по аналогии с открытыми и закрытыми задачами, введем различение профессиональных деятельностей с открытым и закрытым типом успешности. Задачи закрытого типа предполагают только один вариант решения, который является оптимальным и не может быть дальше усовершенствован. Задачи открытого типа имеют множество решений, степень совершенства которых сверху не ограничена.

Если обратиться к миру профессий, то очевидно, что, например, деятельность рабочего у конвейера, контролера в общественном транспорте или кассира имеет закрытый тип успешности. При низком уровне компетентности эта деятельность не достигает оптимума успешности и характеризуется большим количеством брака. Однако по достижении определенного уровня компетентности успешность достигает потолка и далее не возрастает.

Профессии закрытого типа успешности могут быть весьма разными по когнитивной сложности и требовать разных уровней компетентности и необходимой для ее приобретения способности. Если работа у конвейера обычно не рассматривается как требующая интеллекта выше среднего, то деятельность, например, нотариуса, согласно американским правилам профессионального отбора, предполагает интеллект, превышающий средние значения более чем на одно стандартное отклонение (Gottfredson, 1997). Тем не менее нотариус или же бухгалтер – тоже профессии с закрытым типом успешности: после достижения определенного уровня профессиональной компетентности прирост успешности прекращается. Суть этих профессий – проведение действий в соответствии с установленными нормами. Если нормы выполняются, деятельность должна быть признана успешной, и далее ее успешность не повышается ввиду того, что превышать нормы не требуется или даже противопоказано.

В то же время вроде бы близкая деятельность адвоката не имеет четкого потолка успешности. Возможность влиять на суд в пользу своих подзащитных выдвигает из среды адвокатов таких выдающихся личностей, как Плевако или Кони. Аналогично, например, в сфере науки продуктивность ученого не ограничена сверху, и вклад талантливых личностей в ее развитие многократно превосходит среднестатистический уровень. Только что обсужденный аспект модели имеет любопытные следствия. Если способности нормально распределены в соответствии с гауссовым законом, то треугольный характер зависимости, представленной на рисунке 1.1, будет приводить к возникновению левосторонней асимметрии распределения компетентностей, как это показано на рисунке 1.2 (см.: Дружинин, 2002).

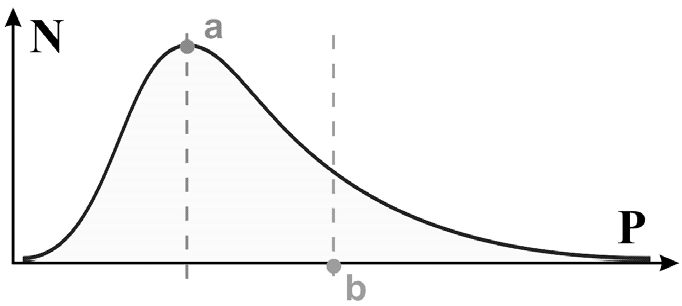
Рис. 1.2. Левосторонняя асимметрия распределения компетентностей

Если сопоставить асимметрию распределения компетентностей, изображенную на этом рисунке, и соотношение компетентностей и достижений в профессиональной деятельности открытого типа успешности, можно придти к выводу, что в наиболее творческих профессиях следует ожидать резкую асимметрию распределения достижений. Это означает, что в таких профессиях значительную часть продукта производит относительно небольшая часть занятых в них людей. Собственно, это совпадает с эмпирически установленными закономерностями.

Еще в конце XIX в. социолог Парето установил, что 80 % доходов в Англии того времени получали 20 % населения и нашел схожее распределение для других стран и времен. Хотя из асимметрии распределения трудовых вкладов и должна следовать асимметрия доходов, обратное неверно. Кроме того, распределение Парето оказалось применимым к очень широкому кругу феноменов – от функционирования компьютерных процессоров до систем контроля качества на производстве. В этом смысле его трактовка как следствия асимметрии трудовых вкладов представляется необоснованной, хотя применение принципа Парето к распределению трудовых вкладов на предприятиях может рассматриваться как достаточно правдоподобное.

Существуют, однако, другого рода оценки – связанные с закономерностями, которые были обнаружены в творческих профессиях. Так, согласно закону Прайса (Price, 1963), половина всех произведений в данной области создается группой, численность которой равна корню квадратному из общего числа членов данного сообщества. Например, если классический музыкальный репертуар образован произведениями примерно 250 композиторов, то половина этого репертуара принадлежит корню квадратному из 250, т. е. примерно 16 композиторам, что и обнаруживает эмпирическое исследование (Moles, 1968). Функция распределения продуктивности в любой сфере творчества оказывается резко асимметричной, причем асимметричность увеличивается с ростом выборки. Для разумных объемах выборки асимметрия оказывается существенно выше, чем в случае распределения Парето.

На основании изложенных положений модели можно выдвинуть следующее дополнительное предсказание: увеличение значимости наиболее сложных и творческих компонентов в деятельности будет приводить к нарастанию асимметрии. Это предсказание до сих пор не проверялось, однако допускает эмпирическую проверку. Например, можно предположить, что периоды «научных революций» в смысле Т. Куна требуют более неординарных подходов, чем периоды «нормального развития науки», и, следовательно, будут приводить к более выраженной левой асимметрии распределения научного продукта, в том числе измеряемого – публикаций.

Из сказанного вытекает объяснение большей асимметричности распределения Прайса, чем распределения Парето. Если распределение Парето можно рассматривать как описывающее распределение вкладов на средней корпорации, то распределение Прайса относится к «верхним этажам» человеческого творчества. Из излагаемой модели следует, что во втором случае асимметрия должна быть больше.

Данный текст является ознакомительным фрагментом.