Построение формальной модели

Построение формальной модели

Изложенные положения модели дают основания перейти к ее формализации[7]. Эта формализация имеет двоякое значение. Во-первых, в практическом плане она открывает путь к количественным оценкам и тем самым сообщает модели предсказательные возможности. В частности, она позволяет дать экономические оценки различным сценариям работы с одаренными детьми. Во-вторых, в исследовательском плане формализация ускоряет процесс совершенствования теории, поскольку позволяет формулировать точные предсказания, соотнесение которых с действительностью выявляет нестыковки в теории и заставляет вносить в последнюю изменения. В то же время любая формализация связана со схематизацией, отбрасыванием части «пышно зеленеющего древа жизни» в пользу сухой теории. В особой степени это касается ее начальных этапов, когда закладываются принципы схематизации для той или иной области. Поэтому представляется, что оптимальным путем сегодня является сочетание двух подходов – номотетического, стремящегося к созданию абстрактных моделей, и идеографического, сохраняющего богатство живого представления о человеческой личности.

Вначале необходимо ввести функции, отображающие способности на компетентности и компетентности – на экономические достижения. Первая описывает, каким образом у групп людей, включенных в экономический процесс, на основе способностей формируются компетентности, и фактически является показателем работы образовательной системы страны. Функция, отображающая компетентности на экономические достижения, характеризует экономическую систему государства, а именно востребованность в ней высококомпетентных специалистов.

Для наших целей удобно сразу использовать одну функцию, являющуюся композицией двух перечисленных, поскольку при этом можно воспользоваться данными Р. Линна, которые приводят в соответствие способности и экономические достижения.

Для удобства последующих расчетов преобразуем оси интеллекта I и экономических показателей D таким образом, чтобы все данные Линна уместились в отрезках [0, 1]. Это достигается за счет следующего преобразования:

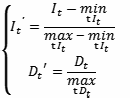
где индекс t обозначает соответствующую страну в данных Линна. Далее будем работать в новых осях, поэтому штрихи учитывать для удобства не будем.

Рассмотрим два варианта аппроксимации: при помощи степенной функции и при помощи показательной функции, которую предлагает Дикерсон (Dickerson, 2006). Мы пойдем по двум путям отдельно, а потом сравним полученные результаты.

Все степенные и показательные функции представим в виде трехпараметрического семейства:

F₁(I; k, m, a) = m(I – a)^k,

F₂(I; k, m, a) = m ? k^{(I – a)}.

Будем искать соответствующие функции f₁(I) и f₂(I) методом наименьших квадратов:

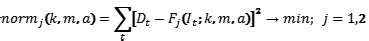
Следует отметить, что данные Линна имеют различную надежность для разных стран. Для большей части стран они основываются на эмпирических исследованиях, охвативших выборки большего или меньшего размера. Однако Линн расширяет свой список путем добавления стран, для которых интеллект оценен косвенно, в частности, путем сопоставления с интеллектом в соседних странах. Таким образом, мы располагаем менее обширным списком стран, для которых оценки интеллекта более надежны, и расширенным списком, для которого, однако, оценки интеллекта менее надежны. Расчеты были проведены отдельно по полному списку и – по сокращенному. В последний были включены страны, где данные по интеллекту были получены на выборке не менее 400 человек.

Линн сопоставляет свои данные по интеллекту с показателями ВВП за 2002 г. Более на дежно, однако, брать данные по ВВП не за один год, а за несколько, поскольку этим снижается влияние краткосрочных экономических факторов. Соответственно мы осуществили расчеты как на основании приводимых Линном данных за 2002 г., так и на основании усредненных показателей за 2002, 2006 и 2007 гг. Данные за 2006 г. были взяты с сайта Международной организации здравоохранения (World Health Organization), а за 2007 г. – с сайта Всемирного банка (World Bank). Данные за 2006 и 2007 гг. удалось получить не по всем странам, представленным в списках Линна, поэтому краткий список сократился на 6 стран, а расширенный – на 10. Из всех выборок исключены Китай и Экваториальная Гвинея.

Результат решения задачи для разных вариантов данных суммирует таблица 1.4.

На основании данных, представленных в таблице, можно заключить, что наиболее точно связь национального интеллекта и доходов на душу населения аппроксимирует степенная функция с показателями, варьируемыми от 2,08 до 2,6 для разных вариантов данных. Однако если взять показатель степени, равный 2, то полученная квадратичная функция, как видно из таблицы 1.4, аппроксимирует данные лишь чуть хуже, чем степенная с оптимально определенным показателем степени, и примерно так же (а для данных с достоверными коэффициентами интеллекта даже лучше), как это делает показательная функция. Стоит отметить, что точность аппроксимации в случае усредненных доходов на душу населения по трем годам оказывается выше, чем для одного года.

Далее мы проведем расчеты на основании двух моделей – квадратичной и степенной, а затем сравним сходство вытекающих из них оценок. Эти модели являются наиболее контрастными, поскольку степенная предполагает наиболее быстрый рост функции при возрастании аргумента, а квадратичная – наиболее медленный. Следовательно, степенная модель будет давать наиболее высокие оценки экономическому вкладу одаренной части населения, а квадратичная – самые низкие. В связи с этим, если оценки, полученные на основании двух моделей, окажутся достаточно близкими, это станет свидетельством высокой стабильности результатов, получаемых на основании предложенного подхода.

Таблица 1.4. Аппроксимация связи национального интеллекта и доходов на душу населения

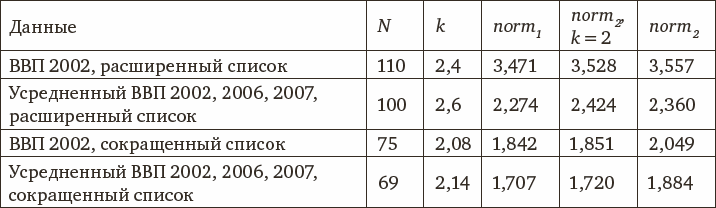
Примечание: N – количество стран, k – полученный в результате решения задачи коэффициент степенной функции. В остальных трех столбцах отображены полученные нормы соответственно для степенной модели, для степенной модели с заданной степенью равной 2 и для показательной модели.

Данный текст является ознакомительным фрагментом.