Арифметика
Арифметика
Операции с числами от 1 до 10
Д ля обучения четырем основным арифметическим операциям необходим следующий материал: штанги разной длины, которые материализуют для ребенка числа 1, 2, 3,4, 5,6,7, 8, 9,10. Каждая штанга разделена на отрезки, контрастные по цвету, красные и голубые. Количество отрезков соответствует определенному числу. Идея представить число единым предметом, содержащим очевидные признаки, позволяющие узнать нужное число, а не набором отдельных счетных единиц облегчает вхождение в суровый и сложный мир чисел.
Вот число «5» — оно представлено одним предметом, разделенным на 5 отрезков. И это лучше, чем представить его пятью одинаковыми отдельными объектами, которые ребенок должен будет мысленно объединять.
При помощи наших штанг дети с легкостью совершают первые арифметические операции:
7 +3 = 10; 2 +8 = 10; 10-4 = 6
Это превосходный материал, но слишком громоздкий, для него нужно много места, его невозможно раздать всем детям. Вот почему, сохраняя основную идею, мы приготовили более компактный материал, его можно сделать в таком количестве, чтобы хватило на всех учеников в классе (когда все уже увлеклись арифметикой). Для него не нужно много места — ребенок может разложить его на своем столе. Это бусины, нанизанные на прочный стержень. Бусины окрашены в разные цвета. На стержне с десятью бусинами они красного цвета, с девятью — голубого, с 8-ю — белого, с 7-ю — желтого, с 6-ю — зеленого, с 5-ю — коричневого, с 4-мя — сиреневого, с 3-мя — салатового, с 2-мя — фиолетового. Одна черная бусина представляет единицу. Бусины сделаны из блестящего стекла, а стержень из металла. На концах стержня — неподвижные фиксаторы. Эти небольшие наборы уложены в коробки по S наборов в каждой. Следовательно, ребенок получает возможность составлять самые разнообразные комбинации.
Материал имел огромный успех у детей пяти с половиной лет. Они трудились с огромным энтузиазмом, делая до 60 арифметических операций подряд, заполняя целые тетради результатами многодневных вычислений. Для записей мы приготовили ученикам особую бумагу: обычные листы в клеточку, только клеточки нарисованы линиями разных цветов. На одном — черные, на другом — красные, на третьем — зеленые, голубые, розовые, коричневые. Разнообразие цветов привлекает ребенка, делает его работу приятной. Едва записав цифры на одном листочке, малыш хватает следующий, другого цвета, и т. д.
Опираясь на свой опыт, мы приготовили побольше стержней с десятью бусинами, десятков. Дети постоянно доставали из коробки все десятичные стержни и считали десятками: 10, 20, 30, 40… Мы сделали коробки с десятками (полные десятичных стержней). Там же лежали карты, на которых было написано 10, 20, 30… Дети раскладывали на карты нужное количество десятичных стержней. Это прекрасная подготовка к умножению на 10. Карты, на которых написано 100 и 1000, позволяют детям составлять такие большие числа, как 1916. Упражнения с бусинами готовят к устному счету.
Это умение появляется внезапно, словно само собой. Ребенок постепенно перестает пересчитывать бусины, а узнает количество их на стержне по цвету. Красные — значит 10, зеленые — 6. И незаметно начинает считать по цвету, не по бусинкам. То и дело раздается крик: «Я сосчитал в уме! Это гораздо быстрее!» Значит, ребенок уже перешел к следующему этапу, разноцветные бусины ему больше не нужны.
Десятки, сотни, тысяча
Материал. Мы сделали цепь, соединив 10 десятичных стержней. Цепь назвали сотенной. Потом соединили 10 сотенных цепочек при помощи гибких соединений — получилась тысячная цепь. Эти цепи были того же цвета, что и десятичные стержни, — красного. Их длина потрясала. Положим сначала одну бусину (единица), потом стержень с десятью бусинами (длиной примерно 7 см) — десяток, потом сотенную цепь (70 см) — сотня и, наконец, тысячную цепь длиной около 7 метров. 1,10, 100 — можно разложить на столе, исследовать с удобством. Для тысячной цепи не хватит и целого класса. Придется выйти в коридор, даже во двор. Одному человеку не под силу разложить тысячную цепь — несколько ребятишек должны терпеливо растягивать ее, а потом нужно еще пройти много шагов, чтобы увидеть цепь целиком.
Это ощущение соотношения величин становится настоящим событием для детей. Целыми днями дети увлеченно возятся с тысячной цепью. Гибкие соединения после каждой сотни позволяют складывать ее. Можно, укладывая сотню над сотней, соорудить длинный прямоугольник и увидеть площадь величины, представленной сначала как длина.
Вы спросите, как помочь ребенку количественно оценить соотношение величин, интуитивно воспринимаемое на глаз. Мы задавали себе тот же вопрос. Тем бременем ученики были заняты подсчетом бусинок, одну задругой, терпеливо, от 1 до 100, сгрудившись кучей над тысячной цепью. Ничто в мире не могло поколебать их решимости сосчитать бусины на этой громадине. «Сто, а что потом?» — «Сто один». — «А после двухсот?» — «Двести один». Дошли до семисот. «Я устал, — говорит малыш, — я оставил метку, завтра досчитаю». Семьсот, семьсот… «Смотри, — говорит ребенок приятелю, — это семь, семь сотен. Да! Можно считать сотенные цепи! Семь сотен, восемь сотен, девять сотен и тысяча. Мадам! Мадам! В тысячной цепи 10 сотенных! Вот они!» Остальные ученики, работавшие с сотенными цепями, вдруг обнаруживают: «Смотрите! В сотенной цепи 10 десятичных стержней!» Значит, можно дать представление о десятках, сотнях, тысячах, предоставив пытливому детскому уму цепи из бусинок и уважая свободное проявление детской активности.
Именно так случается чаще всего, иногда требуется самое незначительное вмешательство взрослого. Достаточно привлечь внимание к манипуляции с цепью — идея предстает во всей своей простоте.
Сторонники нашего метода, впрочем, умеют ждать, они понимают, как нужна ребенку неспешная умственная работа, насколько естественно и неожиданно может созреть идея, как неизбежен взрыв открытия. Чем больше мы предоставляем детей их интересу, тем большую ценность обретают полученные ими результаты.
Счеты, отражающие десятичную систему
Непосредственное вмешательство учителя, его короткое, понятное объяснение необходимы для представления другого материала, который, можно сказать, символически представляет десятичную систему. Речь идет о счетах, очень простых. Они того же размера, что и рамки со шнуровками для малышей, легкие, ими просто манипулировать, несложно и недорого изготовить. Каждому ученику можно дать собственные счеты в личное пользование.
Счеты первой разновидности — малые. На четырех горизонтальных металлических спицах нанизаны бусины, по 10 на каждой. Три верхние спицы расположены на одинаковом расстоянии, нижняя — гораздо дальше от остальных, она выделена металлической шишечкой, закрепленной на левой стороне рамки. Сама рамка ниже этой шишечки выкрашена в один цвет, выше — в другой. На левой стороне рамки рядом с местом крепления каждой спицы написаны числа: рядом с верхней спицей — 1, со второй — 10, с третьей — 100, рядом с нижней, отдельной спицей — 1000.
Мы объясняем ребенку, что считаем каждую бусину на верхней спице единицей, как всякую отдельную бусину (здесь бусины зеленые). Каждая синяя бусина на второй спице представляет сразу десяток (как десятичный стержень), красная бусина на третьей спице — сотня (сотенная цепь), зеленая бусина на четвертой спице — тысяча, она равна тысячной цепи.
Конечно, освоить эту символику детям непросто, однако, если мы дадим им время спокойно разглядывать счеты, считать бусины, изучать цепи, они, в конце концов, во всем разберутся. Идея соотношения единицы, десятка, сотни, тысячи созреет в них постепенно, ученики поймут смысл символики, научатся ею пользоваться.
К счетам прилагаются расчерченные листочки. Они поделены вертикальной линией на две равные части. И на правой, и на левой части проведены вертикальные параллельные линии на равном расстоянии: крайняя справа — зеленая, затем синяя, затем красная. Пунктирная линия отделяет эту группу от еще одной вертикали, проведенной на большем расстоянии (сдвинутой влево). На трех первых вертикалях пишут (справа налево) единицы, десятки, сотни, на отдельной вертикали после пунктира — тысячи. Правая сторона листочка предназначена для объяснения данной идеи, для установления связи между записью и счетами, символизирующими десятичную систему.
Сначала можно посчитать бусины на счетах, приговаривая: «Первая спица: одна единица, две единицы, три единицы, четыре единицы, пять единиц, шесть единиц, семь единиц, восемь единиц, девять единиц, десять единиц. Все десять единиц равны одной-единственной бусине на нижней, второй спице». Так же считаем бусины на второй спице: «Один десяток, два десятка, три десятка, четыре десятка, пять десятков, шесть десятков, семь десятков, восемь десятков, девять десятков, десять десятков. Все десять десятков, десять бусин второй спицы равны одной бусине на нижней, третьей спице». Так же считаем бусины на третьей спице: «Одна сотня, две сотни, три сотни, четыре сотни, пять сотен, шесть сотен, семь сотен, восемь сотен, девять сотен, десять сотен. Все десять сотен, десять бусин третьей спицы равны одной бусине на нижней, четвертой спице». Тысячных бусин тоже 10: «Одна тысяча, две тысячи, три тысячи, четыре тысячи, пять тысяч, шесть тысяч, семь тысяч, восемь тысяч, девять тысяч, десять тысяч». Ребенок может представить себе десять тысячных цепей. И символ соединится с зрительным представлением о количестве.
Теперь нужно как-то записать все наши счетные действия. На правой вертикальной линии (зеленой) мы пишем единицы, одну под другой. На второй вертикали (синей) — десятки (столбик располагается ниже единиц), на третьей вертикали (красной) — сотни (еще ниже). На четвертой вертикали, отделенной пунктиром, — тысячи (внизу листа). Горизонтальные линии листочка позволяют спускаться постепенно от единиц до тысячи.
Вот мы написали цифру 9 на зеленой единичной вертикали. Теперь мы переходим от единичной вертикали к десятичной, пишем там цифру 1. Действительно, 10 единиц — один десяток. Написав 9 на десятичной вертикали (синей), переходим к сотенной линии (красной). Написав 9 на сотенной линии, переходим к тысячной, потому что, в самом деле, 10 сотен — это тысяча. Цифры закономерно сменяют друг друга (от 1 до 9), затем — переход. Эта идея должна созреть в сознании детей. Девять цифр, меняя места, способны выразить любое число в мире! Не цифра сама по себе, ее место по отношению к другим придает ей определенное значение. Иногда это 1, иногда 10, или 100, или 1000. И так до бесконечно огромных величин, которые мы и представить себе не можем. У нас есть тысячная цепь — ее длина 70 метров. А десятитысячная цепь, десять тысячных цепей, была бы длиной с целую улицу. Вот для чего нужны символы. Вот как важно место цифры в числе!
Но как мы указываем место цифры по отношению к другим цифрам, как определяем ее значение? Ведь не всегда есть разноцветные вертикальные линии. Люди ставят ноль справа от цифры. Наши ученики еще раньше узнают, что такое ноль — ничто, он ничего не прибавляет к числу, но способен указать его место и, таким образом, дать нам представление о его значении. Именно ноль, стоящий справа, превращает единицу в десяток. Ноль в «10» нужен, чтобы показать, что цифра один означает не единицу, она занимает место на линии десятков. Если вместо «0» будет стоять, например, «4», значит, у нас 4 единицы и один десяток.
Наши дети еще до школы умели писать 10, 100, поэтому им теперь так легко писать при помощи ноля в столбик, считая от 1 до 1000:1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 200, 300, 400, 500, 600, 700, 800, 900, 1000. Научившись так считать, дети могут прочесть четырехзначное число.
Составим число сначала на счетах, например, 4827. Сначала откладываем влево четыре бусины на нижней, тысячной спице, 8 — на сотенной, 2 — на десятичной и 7 — на спице с единицами. Читаем: 4827.
Теперь записываем цифры на вертикальных линиях. Так же можно поступить и с числом, обозначающим год нашей жизни — 1916. Теперь отложим на счетах 2049. Сначала откладываем влево две бусины на нижней, тысячной спице, 4 — на десятичной и 9 — на спице с единицами. На сотенной спице ничего не отложено. Вот демонстрация роли ноля. Он нужен, чтобы обозначить пустое место.
То же самое с числом 4700, составленном на счетах. Сначала откладываем влево четыре бусины на нижней, тысячной спице, 7 — на сотенной, на остальных спицах — ничего. При записи эти пустые места мы заполняем нолями, то есть цифрами, которые ничего не значат.
Едва ребенок разобрался в этом, он самостоятельно начинает тренироваться с огромным интересом. Он откладывает влево наугад бусины на некоторых спицах на счетах, а потом старается понять, какое число получилось, и записать его на вертикальных линиях листочка. Эти операции с многозначными числами, с записью столбиком вполне доступны ребенку, если дать ему возможность самостоятельно упражняться.
Очень скоро ребенок захочет выйти за пределы тысячи.
Тогда понадобятся вторые счеты, большие. У них 7 спиц: единицы, десятки, сотни простые; единицы, десятки, сотни — тысяч и, наконец, — миллион. Переход от малых счет к большим вызывает огромный интерес и никаких трудностей. Детям практически не нужны комментарии учителя, они стараются сами во всем разобраться. Их страшно увлекают большие числа, и у них не возникает особых проблем. Скоро в классе появляются тетради, заполненные фантастически огромными числами. Дети с легкостью оперируют семизначными величинами!
Большие счеты располагаются в такой же рамке, что и малые. Левая сторона рамки выкрашена в три цвета, в соответствии с группами спиц. Единицы, десятки и сотни отделены шишечкой от тысячной группы, тысячная группа отделена шишечкой от миллионной спицы.
На разлинованном листе бумаги мы пишем в правой части числа от одного до миллиона: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 200, 300, 400, 500, 600, 700, 800, 900, 1000, 2000, 3000, 4000, 5000,6000, 7000, 8000,9000,10 000, 20 000, 30 000,40 000, 50 000,60 000, 70 000, 80 000, 90 000, 100 000. (По аналогии с листочком, входящим в комплект с малыми счетами.)
Теперь ребенок откладывает на счетах бусины, старается прочитать число и записать его на линеечках. Числа сумасшедшие: 6 206 818, 1 111 111,8 640 850 и т. д.
Когда придет время складывать или вычитать в столбик, ребенок будет удивлен легкостью, с которой сумеет овладеть этими операциями.
Таблица Пифагора
(Таблица умножения)
Материал: белая квадратная доска со ста ячейками (10x10). В каждую можно положить бусины. Сверху над каждым столбиком ячеек написаны числа от 1 до 10. Слева есть отверстие, куда можно вставить одну из маленьких карточек с красной цифрой, от 1 до 10 (нужно приготовить 10 Таких карточек). Это второй сомножитель, его можно менять. В левом верхнем углу есть отверстие, где лежит красный жетончик, но это второстепенная деталь. Края доски выкрашены в красный цвет. Коробка с сотней бусин входит в комплект. Само упражнение чрезвычайно простое.
Предположим, мы хотим умножить 6 на серию натуральных чисел, от 1 до 10. Вставляем в левое отверстие маленькую карточку с цифрой 6.6x1. Ребенок делает две вещи: кладет красный жетон на единицу, написанную в верхнем ряду, и 6 бусин в ячейку под ней. 6x2. Ученик перемещает красный жетон на цифру 2, добавляет 6 бусин в ячейку второго столбика, под двойкой. То же самое с умножением 6x3. Жетон перекладываем на «3», добавляем 6 бусин в ячейку третьего столбика. И так вплоть до 6x10.
Перемещение жетона указывает на множитель и привлекает внимание ребенка, помогает ему сохранять сосредоточенность и точность исполнения. Выполняя все эти операции, ученик записывает полученные результаты. Для этого существуют специальные листочки, по 10 на каждую серию, в системе 10 серий, следовательно, всего 100 листочков. Вот листочек, приготовленный для умножения на 3.
На листочке все написано заранее. Ребенку остается только вписать полученные результаты, прибавляя каждый раз по 3 бусины. Если ученик не ошибется в подсчетах, то запишет: 3, 6, 9, 12,15, 18, 21, 24, 27, 30. И так в каждой серии листочков, от 1 до 10. У каждого листочка есть 10 копий, поэтому каждое упражнение ребенок может повторить 10 раз. Вскоре он заучивает наизусть эти результаты. Мы видели, как, стараясь выучить таблицу умножения поскорее, дети расхаживают по классу с листочком в руках, то отводя от него взгляд, то заглядывая в правильные ответы, и шепчут: 7x7=49,7x8=56. Этот листочек написали они сами.
Таблица Пифагора оказалась одним из самых увлекательных материалов. Дети заполняли по 6, 7 листков подряд, посвящая целые дни и недели упражнениям на умножение. Почти все просили разрешения забрать таблицу домой. Однажды даже случилась небольшая революция. Все хотели забрать материал домой, но мы не разрешали это сделать. Дети стали умолять родителей купить им вожделенный материал. Невозможно было им объяснить, что такие вещи не продаются в магазине, их нельзя купить. Ученики не сдавались. Нашлась девочка, самая старшая из всех, которая возглавила восстание. «Учительница ставит над нами эксперимент. Отлично! Если она не даст нам таблицу Пифагора, мы завтра не придем в школу!» Конечно, подобные угрозы звучат не очень красиво, но посмотрите, какое впечатление произвел наш материал на класс, как быстро превратил он агнцев в волков.
Заполнив много раз все серии листочков, дети получают проверочную таблицу, чтобы увидеть, нет ли ошибок в их записях. Цифра за цифрой, столбик за столбиком, они сверяют все полученные результаты. Теперь у них есть безошибочная таблица умножения.
Затем ученики переписывают ее в подготовленный квадрат.
Таблица Пифагора
Таблица Пифагора
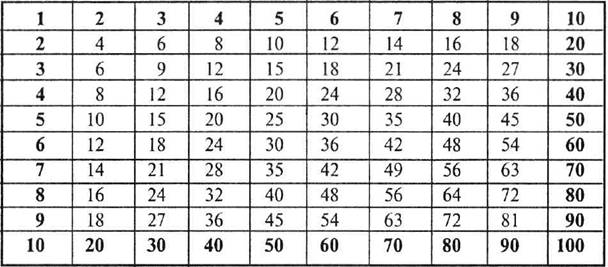
Ребенок получает таблицу Пифагора как результат усиленной работы. Теперь нетрудно научить его воспринимать ее как таблицу умножения. Он уже знает ее наизусть, может заполнить пустые клеточки по памяти. Единственная трудность — понять, в какой клеточке писать число, то есть какая цифра множимое, а какая множитель. В каждый комплект входит 10 пустых таблиц, ребенок может упражняться, сколько хочет, он осваивает процесс. В итоге он знает таблицу умножения наизусть.
Деление
Материал: та же доска, бусины, только другие листочки.
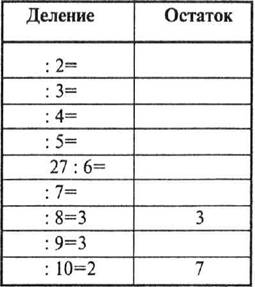
Возьмем наугад любое количество бусин из коробки и сосчитаем их. Предположим, получилось 27. Это число вписываем в левой части листочка, в разделе деление. Теперь берем доску с ячейками и приступаем к делению. Сначала делим 27 на 10. Кладем 10 бусин в ячейку вертикального столбика под цифрой 1. Затем еще 10 бусин рядом, в ячейку вертикального столбика под цифрой 2. Нам не хватает бусин, чтобы положить их в ячейку вертикального столбика под цифрой 3. Нужно 10, а осталось 7. Значит, пишем цифру 2 на листочке в разделе деление на соответствующей строке и на той же строчке справа, в разделе остаток, пишем цифру 7 — то, что осталось. Теперь будем делить на 9. Кладем 9 бусин в ячейку вертикального столбика под цифрой 1, потом под цифрой 2, потом под цифрой 3. Бусин больше не осталось. В левой части листочка на соответствующей строке пишем цифру 3, в графе остаток ничего не пишем. Делим на 8. Кладем 8 бусин в ячейку вертикального столбика под цифрой 1, под цифрой 2, под цифрой 3. Для четвертой ячейки бусин не достаточно, осталось только 3 (а нужно 8). Результат — 3 и 3 в остатке. И так далее.
100 листочков для деления мы положили в зеленый конверт. Листочки для умножения (а также проверочные таблицы и таблицы Пифагора) лежат в пергаментном конверте.
Операции с многозначными числами
Теперь у нас все готово для операций с многозначными числами. Ребенок умеет обращаться с материалом, его ум готов.
Для сложения, вычитания и умножения нам понадобятся счеты, а для деления более сложный материал, который мы опишем позже.
Сложение
Сложение многозначных чисел на счетах — что может быть проще и увлекательнее! Например,
1320 +
435 =
Сначала отложим бусины, соответствующие первой цифре первого числа, то есть 1 на спице тысяч. На сотенной спице — 3, на десятичной — 2. Теперь откладываем бусины второго числа, присоединяя их к уже отложенным бусинам первого числа: 4 на сотенной спице, 3 на десятичной и 5 на единичной. Осталось только записать полученное число, подсчитав все отложенные бусины: 1755.
Теперь возьмем более сложный случай, когда нам понадобится отложить на спице больше 10 бусин. На самом деле, ничего сложного. Дойдя до 10, мы возвращаем на место все бусины на данной спице и откладываем одну на нижней (на Ней одна бусина равна 10 бусинам верхней спицы). И продолжаем процесс.
Вот пример:
390 + 482 =
Сначала откладываем число 390, то есть 3 бусины на сотенной спице и 9 на десятичной. Теперь второе число: 4 бусины на сотенной спице, переходим к десяткам. Отложили всего одну бусину — и на спице ничего не осталось. Возвращаем все бусины на место, откладываем одну бусину на нижней спице, сотенной, и продолжаем откладывать десятки, еще 7 бусин (одну из 8 мы уже отложили). Осталось отложить 2 бусины на единичной спице. Операция закончена. Результат: 872. На больших счетах можно таким же образом совершать и более сложные операции.
Считать не обязательно с наибольшего разряда, можно начинать и с единиц, как удобнее ученику.
Вычитание
Нам понадобятся те же счеты. Например, мы хотим сосчитать, сколько будет 8947 -6735-
Сначала откладываем бусины первого числа, а потом возвращаем на место столько бусин, сколько входит во второе число. Оставшиеся отложенными бусины — это и есть наш результат: 2212.
Более сложный случай — переход через десяток. Если одна спица опустела, мы возвращаем на место одну бусину с нижней спицы и откладываем все десять бусин на верхней. И продолжаем операцию. Например:
8954 -7593 =
Откладываем бусины первого числа. Теперь отнимаем 3 единичные бусины. На десятичной спице начинаем отнимать 9 бусин… Отняли 5 — спица опустела. А нам нужно отнять еще 4. Отнимаем одну бусину на нижней сотенной спице и возвращаем на место сразу все 10 бусин десятичной спицы, теперь нам есть, от чего отнимать оставшиеся 4 бусины (5 из 9 мы уже отняли). От сотен (на этой спице осталось 8 бусин) отнимаем пять, и т. д. Результат 1361.
Умножение
Переходить к умножению многозначных чисел надо не раньше, чем ребенок выучит таблицу умножения, научится хорошо отличать единицы, десятки, сотни, выучит цифры и связь их положения в числе со значением. Он должен привыкнуть к переходу через десяток, освоить его как совершенно обычное дело.
Тогда достаточно будет сказать ученику, что каждая цифра множимого должна быть умножена на каждую цифру множителя, а результаты умножения нужно сложить. Здесь гораздо важнее использовать аналитический процесс для развития интеллекта ребенка.
Каждое число, обозначенное цифрой, в первом числе умножается на каждое число, обозначенное цифрой, во втором числе.
Вот пример:
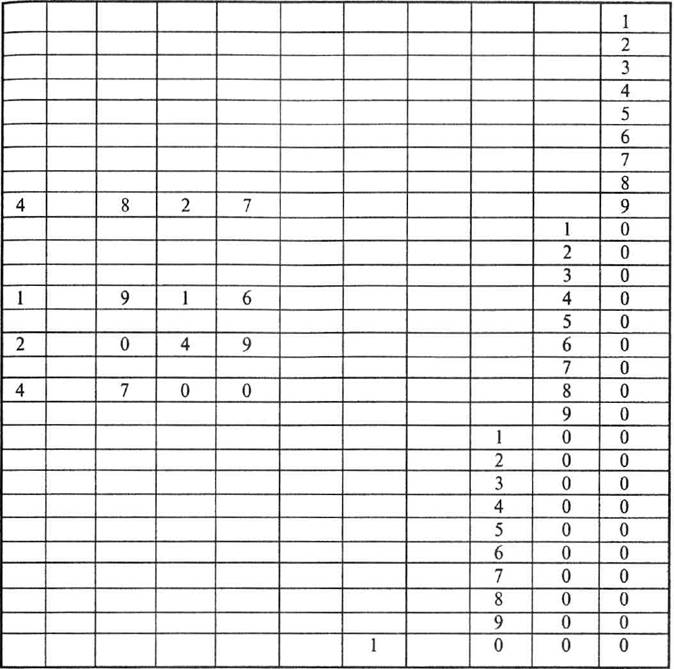
356 х 742.
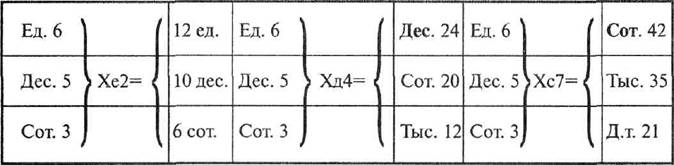
Написав такой анализ, начинаем работу на больших счетах. 2x6 единиц — откладываем 10 бусин на единичной спице, но этого мало, возвращаем на место единичные бусины, откладываем одну десятичную на нижней спице, а единичных — 2.
Теперь 2x5 десятков. У нас уже отложена одна десятичная бусина. А к ней надо прибавить еще 10. Придется отложить одну бусину на сотенной, нижней спице. Сейчас у нас отложена 1 сотенная, 1 десятичная и 2 единичные бусины.
Умножаем 2x3 сотни. Откладываем 6 бусин на сотенной спице. Умножение на единицы закончено.
Переходим к умножению на десятки. Все происходит аналогично, только начинается сразу со второй спицы, с десятичной.
Мы прибавляем бусины к уже отложенным. Результат — 264 152.
Описывать очень сложно — проделывать все это на счетах крайне увлекательно. Настоящая арифметическая игра, которая к тому же помогает не только освоить десятичную систему, но и абстрактные операции, развивает способность к абстрагированию.
Действительно, если умножать в столбик, смотреть на цифры, записанные на бумаге, ничего не почувствуешь. Бусины движутся, значение каждого числового разряда ощущается через механическое движение руки. К тому же писать цифры сложнее, чем откладывать бусины на счетах, они скользят так легко по гладкой спице. Счет на бумаге менее ясен. Привыкнув упражняться на счетах, ребенок уже машинально откладывает бусину на нижней спице, перейдя через десяток, он не забудет «3 в уме». Вообще не нужно ничего держать в уме, все отложенные бусины остаются на спице, перед глазами, их можно снова пересчитать. Ученик не ошибется в подсчете результата, ему не придется писать бесконечные нули при умножении 3400 на 2. Он просто отложит 6 бусин на тысячной спице и 8 на сотенной. К тому же на счетах не так важен порядок операций, можно сначала умножить на десятки, а потом на единицы. На бумаге это труднее.
Счеты развивают также ручную моторику. В конце концов, можно устраивать соревнования, кто быстрее умножит числа: тот, кто работает на счетах, или тот, кто считает в столбик на бумаге.
Умножение на бумаге
Возьмем такой пример: 8640x2531. Запишем числа одно под другим, разряд под разрядом. Мы помним, что для обозначения пустого разряда используется ноль. Ноль справа от цифры означает перемещение в следующий разряд.
Умножать такие большие числа, и даже больше, могут легко семилетние дети после вышеописанных упражнений. Количество знаков в числе не имеет значения, ученикам нравится работать с фантастически огромными числами. У нас они сами придумывают себе примеры с 8-значными числами. Учителю и в голову бы не пришло дать им такие числа. Со временем они начинают считать, как все мы, в столбик, без специальных листков и без счет, но понимание сути процесса у них глубже.
Деление многозначных чисел
Бусины позволяют заниматься делением на многозначные числа, это замечательное времяпрепровождение, например, когда ребенок сидит дома. Это умственная, абстрактная арифметика, а не механические операции, превращающие высшую мыслительную деятельность в рутину. Здесь нам понадобятся не счеты, а квадратная доска, та же самая, которую мы использовали для первых упражнений на умножение и деление на однозначные числа. Только нужно приготовить больше карточек и бусин. Работа слишком сложная для описания, но выполняется она с удовольствием и без усилий.
Единицы, десятки, сотни выкрашены в разные цвета: бусины — единицы белые, десятки — зеленые, сотни красные. Есть еще маленькие разноцветные подставки: белые для единиц, десяток, сотен, серые для тысяч, черные для миллионов, а также коробки снаружи белые, серые и черные, а внутри белые, или зеленые, или красные. К каждой коробке приложена подставка с десятью футлярами, по 10 бусин в каждом. Предположим, надо разделить 87 632 на 64. Расставляем в ряд 5 коробок: крайние слева — две серые коробки, одна зеленая внутри, другая белая, затем три белые коробки, одна внутри красная, следующая зеленая, крайняя правая — белая. В первую кладем 8 зеленых бусин, во вторую 7 белых, в третью 6 красных, в четвертую 3 зеленые бусины, в пятую — 2 белые бусины. За каждой коробкой стоит соответствующая подставка с 10 футлярами с бусинами, чтобы менять единицы одного разряда на другой. Квадратные доски (их 2) лежат под вереницей коробок, в левой в прорезь для карточек вставлена карточка с цифрой 6, в правой — карточка с цифрой 4.
Итак, делим 87 632 на 64. Ставим крайние левые коробки (с 8 и 7 бусинами) над квадратными досками. На первой раскладываем 8 бусин в ячейки так, как будто делим их на 6. На второй раскладываем в ячейки 7 бусин, деля на 4 (в соответствии с цифрой на маленькой карточке, вставленной в прорезь). Целые частные выравниваются по первой доске и записываются в соответствующий разряд, остаток остается. Частное в данном случае — 1 (разряд тысяч) и на первой, и на второй доске. На первой доске остаток — 2, на второй — 3. Теперь передвигаем коробки влево. Первая вышла из игры, ее место заняла вторая. Теперь над первой доской не серо-зеленая коробка, а серо-белая, а над второй доской (с цифрой 4) красная коробка. Итак, на первой доске (с цифрой 6) отложены две зеленые бусины, но над ней коробка с белыми бусинами. Значит, нужно поменять зеленые бусины на белые. Кладем 2 футляра по 10 белых бусин, сюда же помещаем остававшиеся на второй доске 3 белые бусины. Теперь раскладываем их в ячейки, деля на 6. На второй доске раскладываем 6 красных бусин из соответствующей коробки и делим на 4. На первой доске 23 белые бусины делим на 6. Получаем 3 и 5 в остатке. На второй доске 6 красных бусин делим на 4. Получаем 1 и 2 в остатке. Как выровнять частные? Для этого берем по одной белой бусине и перекладываем на правую доску, заменяя каждую белую 10 красными, пока частные не сравняются. В данном случае достаточно переложить одну белую бусину. Теперь частное и на второй доске тоже 3 (разряд сотен), а остаток 4. Снова передвигаем коробки и продолжаем делить. То, что останется в самом конце, и есть остаток деления. А записанный на листочке результат потом может проверить учитель.
Работа требует терпения и внимания, но очень интересна детям. Они готовы заниматься ею дома по вечерам, в одиночестве, тихая игра, не утомляющая, не отпускающая.
Поупражнявшись в таком делении, ученик начинает предвидеть результат, не перекладывая бусины. Он научился не только делить, но и глубоко проник в суть операции, каждой ее детали, возможно, лучше, чем ученики средней школы, механически повторяющие заученные действия.
Числовые упражнения (Умножение, деление)
Когда ребенок при помощи наших материалов уяснил идею четырех основных арифметических действий и научился делать их в уме, ничто не мешает углубить знания, возможно, даже подойти к уровню средней школы. Эти упражнения одновременно служат и для повторения знакомого, и для узнавания нового. Они позволяют приятно проводить время в школе и дома.
Одно из первых упражнений является продолжением работы с таблицей Пифагора — умножение в уме, без помощи материальных предметов. В данном случае ставим ограничение. Прекращаем умножение, если результат получается больше сотни. Ради удобства записи будем в первой серии умножать до 50, а во второй (с записью во вторую колонку) от 51 до 1 00. Мы заранее готовим две таблицы, которые служат ученикам и подсказкой, и формой самопроверки. Читать примеры в колонке, сверху вниз, и учить их наизусть — это помогает запомнить результаты умножения всех чисел, от одного до 100.
С таблицами можно делать увлекательные упражнения. Детям дают листы бумаги, узкие и длинные. Слева записаны все числа, от 1 до 50 и от 51 до 100. Ученики смотрят в таблицу и подыскивают примеры, где в результате умножения получается заданное число. После чего ставят знак = и вписывают сомножители. Например, слева напечатано 6. Ставим = и пишем 2x3 = 3x2. Еще пример: 18 = 2x9 = 3x6 = 6x3 = 9x2. Возле некоторых чисел не удастся написать примеры. Строчка останется пустой — получится первое представление о простых числах.
Пример таблицы
Эти таблицы помогают выполнить еще одно упражнение. Например, разглядывая их, ребенок замечает, что 6=2x3 = 3x2. Он берет бусины и раскладывает их то двумя группами по 3, но тремя группами по 2, но одной группой. Для каждого числа он ищет свое расположение бусин.
Ребенок может перебрать все возможные комбинации, испробовать все способы деления числа на равные группы. Дойдя до простых чисел, он уясняет идею делимости и неделимости числа. Кроме того, очевидной становится истина, что от перемены мест слагаемых произведение не меняется. Устанавливается связь между делением и умножением, становится понятно, как одно действие можно проверить другим. Достаточно снова соединить 2 группы по три бусины — получится 6.
Еще одно упражнение мы делаем с узкими листами бумаги. Вот написано произведение — 40. Один из примеров рядом 2x20. Посмотрим, как можно получить 20: 20=2x10, а 10=2x5. То есть
40 = 2x2x2x5.
Можно записать и так: два в кубе умножить на пять. Первое знакомство с возведением в корень.
Еще для одного упражнения готовим квадраты 10x10, где по порядку записаны все числа от 1 до 100, слева направо, сверху вниз:
и так далее.
Жирным шрифтом на разных квадратах выделяем числа, каждый раз выбирая новый принцип, например, все четные числа или все кратные девяти.
Квадрат и куб числа
Берем два стержня бусин по 2 бусины на каждом, соединяем их маленькой цепочкой:
Эта фигура представляет 2x2. Те же самые предметы можно соединить и по-другому. Палочки с бусинами расположить не в ряд, а друг под другом.
Это не изменит их значение, 2x2 все равно 4, но теперь это другое расположение в пространстве: линия и квадрат. Заметим, что всякий раз, располагая друг под другом столько стержней, сколько бусин на них нанизано, мы получим квадрат. Мы приготовили квадраты из стержней с бусинами 3x3 (салатовые), 4x4 (сиреневые), 5x5 (коричневые), 6x6 (зеленые), 7x7 (желтые), 8x8 (белые), 9x9 (голубые), 10x10 (красные), то есть тех же самых цветов, что и стержни с бусинами для освоения числовой системы. Для каждого количества есть стержни с бусинами, соединенные и в цепочки, и в квадраты, и просто свободные стержни (два стержня по две бусины, три — по три и т. д.). Ученик может считать бусины в цепи и в квадрате, а также по-своему располагать свободные стержни, то в ряд, то в форме квадрата. И каждый раз он повторяет число столько раз, сколько единиц в нем содержится, то есть умножает число само на себя.
К примеру, возьмем квадрат 4x4. Можно сосчитать 4 бусины на каждой стороне квадрата, можно умножить 4x4 =16. Это и общее количество бусин, и площадь квадрата. То же упражнение повторяем и с остальными квадратами. Понятно, что результат не зависит от формы. Стержни, вытянутые в линию, все равно дадут тот же результат. Можно научить ребят записывать результат в форме квадрата числа: 22 =4, 52 =25. Материал осваивается с самых малых чисел и постепенно, в сочетании со свободой ребенка, помогает идее проникнуть в сознание ученика.,
Кроме квадратов, по той же схеме созданные, у нас есть кубы чисел и прилагающиеся к ним соединенные в цепь квадраты. В этих цепях стержни соединены гибко, чтобы можно было складывать цепь, накладывать квадраты друг на друга. Количество квадратов в цепи соответствует количеству единиц на каждом отдельном стержне: 4 квадрата для числа 4, 6 квадратов для числа 6 и т. д. — до 10. Эти квадраты можно накладывать друг на друга, а можно и вытянуть в одну линию. Количество бусин не изменится. 4x4x4 = 42х4 = 43 = 64.
Рассмотрим куб подробнее. Одна сторона его состоит из 4 бусин. Умножим 4 раза квадрат со стороной 4 — получим куб. Умножим площадь квадрата на количество единиц, составляющих одну сторону, — получим объем. Мы не стараемся научить этому ребенка, мы просто предоставляем ему свободу действий и даем время на созревание идей в его сознании, пока он играет с материалом, рассматривает его, исследует свой замечательный куб, такой красивый и удобный.
Постепенно в тетрадях детей появляется множество квадратов и кубов чисел. Ученики легко обращают внимание, что при умножении на 10 достаточно просто приписать ноль. Они замечают, что число бусин в квадратах возрастает от двух до ста, а в кубах — до тысячи. Это наблюдение поможет им впоследствии осознать сущность арифметической и геометрической прогрессии.
Из кубов с бусинами интересно строить башню, похожую на розовую башню, только теперь разноцветные кубики соединены для детей с глубоким знанием числовых соотношений. Они не просто воспринимаются на сенсорном уровне, но являются отражением развивающейся мощи интеллекта.
Данный текст является ознакомительным фрагментом.