34. Тестовые нормы. Корреляция качественных признаков
34. Тестовые нормы. Корреляция качественных признаков
Что, несомненно, должен знать и уметь делать каждый грамотный пользователь теста – это понимать, что такое тестовые нормы и как ими пользоваться.
Первоначальный суммарный балл, подсчитанный с помощью ключа, не является показателем, который можно диагностически интерпретировать. Его называют в те-стологии «сырым тестовым баллом». Применение тестовых норм в профессионально организованной психодиагностике основывается на переводе тестовых баллов из «сырой» шкалы в «стандартную». Эта процедура называется «стандартизацией тестового балла».
Допустим, мы провели тест из 20 заданий и испытуемый дал 12 правильных ответов. Можно ли при этом сказать, что способность у испытуемого выражена лучше или хуже, чем в среднем? Нет. Для такого вывода нужно сравнить балл 12 со средним баллом по представительной выборке испытуемых.
Выборка, на которой определяются статистические тестовые нормы, называется выборкой стандартизации. Ее численность, как правило, не меньше 200 человек. Такое количество человек должно принять участие в психометрическом эксперименте по определению тестовых норм – в эксперименте по стандартизации теста.
Корреляция качественных признаков – метод анализа связи переменных, измеряемых в порядковых шкалах и шкалах наименований (см. шкалы измерительные). Наиболее часто такой корреляционный анализ проводят с помощью коэффициентов ранговой корреляции, используемых в случаях, когда обе переменные измеряются в шкалах порядка или легко могут быть преобразованы в ранги. При измерении сравниваемых переменных в шкалах наименований широко применяются коэффициенты сопряженности, в которых в качестве промежуточной расчетной величины используется критерий согласия Пирсона (см. критерий X2). Наиболее часто в таких расчетах пользуются коэффициентом сопряженности Пирсона:
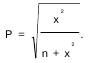
Значение P всегда положительно и измеряется от нуля до единицы. Особенностью коэффициента сопряженности Пирсона является то, что максимальное его значение всегда меньше + 1 и в значительной степени зависит от количества наблюдений (размера таблицы). В случае квадратной таблицы (k x k):
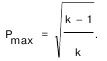
Так, в таблице размером (5 x 5) Pmax = 0,894; в таблице (10 x 10) Рmax = 0,949. Поэтому окончательной формой выражения связи между переменными с помощью коэффициента Пирсона является его отношение к величине Рmax для данного случая (P/Pmax).
При расчете сопряженности находит применение также коэффициент Чупрова:
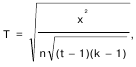
где t – число столбцов таблицы;
k – число строк таблицы.
В психологической диагностике описанные коэффициенты используются относительно редко
Данный текст является ознакомительным фрагментом.