Согласие или отказ заняться сексом
Согласие или отказ заняться сексом
Давайте вернемся к Эмми и Яну. Каждый день один из них предлагает партнеру заняться сексом. Исходя из того, что они получают одинаковые выигрыши, мы получаем следующую матрицу выигрышей:
Ян и Эмми ставят максимальную оценку (5, 5), соглашаясь на секс. Им нравится секс, и они хотят заниматься им как можно чаще. Они ставят друг другу низкие отметки (0, 0), отказываясь от секса. Это имеет смысл. В смешанных ячейках таблицы, где Эмми соглашается, а Ян отказывается, она чувствует себя несчастной, отверженной, поэтому ее выигрыш составляет -1, а выигрыш Яна – 1. Это указывает на то, что она чувствует себя отвергаемой, а он чувствует себя нормально. Этот результат симметричен – если Эмми отказывается, а Ян соглашается, она получает 1, а он – 1. Что выглядит вполне разумной психологической конфигурацией повторяющегося набора вероятностей. Это соответствует ситуации нашей гипотетической пары.
Прекрасно, но существуют ли уравнения Нэша для чистой стратегии – способы для обоих «игроков» получить наилучший результат? На самом деле, есть только один вариант.
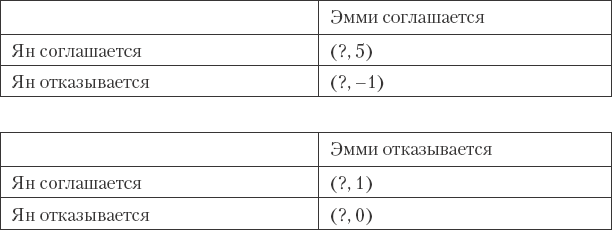
Давайте взглянем на возможные варианты с точки зрения Яна:
Пятерка однозначно получает звездочку. А вот как выглядит таблица, если Ян отказывается заняться сексом:
В данном случае звездочку получает 1.
Вот как выглядит ситуация с точки зрения Эмми:
Здесь звездочку явно получает 5.
Если она отказывается от секса:
На этот раз звездочку получает 1.
Итак, сведем всё воедино:
Следовательно, существует лишь одно уравнение Нэша для чистой стратегии – то, где оба соглашаются на секс. Ничего удивительного!
Все, о чем мы говорили выше, имеет смысл. Но сейчас нам нужно выяснить вероятность того, что каждый партнер согласится на секс, а также ожидаемую частоту занятий сексом для этой пары.
Мы можем вычислить точку безразличия для Яна с помощью приведенных ниже матриц:
И:
ЕР для ЯнаЭмми соглашается = 5?Соглашается + (–1) (1 – ?Соглашается).
ЕР для ЯнаЭмми отказывается = 1?Соглашается + (0) (1 – ?Соглашается).
Пусть ЕР для ЯнаЭмми соглашается = ЕР для ЯнаЭмми отказывается; точка безразличия Яна.
5?Соглашается – 1 +?Соглашается = ?Соглашается.
5?Соглашается = 1.
?Соглашается = 1/5.
Эмми будет соглашаться на секс только в 1/5 всех случаев и отказываться в 4/5 случаев, чтобы Ян был безразличен к ее смешанной стратегии с точки зрения ее ожидаемых выигрышей. А как насчет его смешанной стратегии?
ЕРЯн соглашается = 5?Соглашается + (– 1) (1 – ?Соглашается).
ЕРЯн отказывается = 1?Соглашается + (0) (1 – ?Соглашается).
Пусть ЕРЯн соглашается = ЕРЯн отказывается; точка безразличия Эмми.
5?Соглашается – 1 + ?Соглашается = ?Соглашается
?Соглашается = 1/5
Если Ян использует смешанную стратегию, соглашаясь на секс в 1/5 случаев и отказываясь в 4/5, Эмми будет безразлична к этому с точки зрения ее выигрышей. Прекрасно, мы получили уравнение Нэша для смешанной стратегии. Ура!
Но как часто у этой пары на самом деле будет секс, если исходить из этой матрицы выигрышей? Поскольку оба вынуждены соглашаться на занятия сексом, взаимный показатель согласия составит (1/5) ? (1/5) = 1/25, то есть 0,04 или 4 %. При том что в году 365 дней, пара будет заниматься сексом 15 дней в году (примерно раз в три недели). Это удивительно низкий показатель для такой пары, потому что они разработали разумную с точки зрения психологии таблицу. Что происходит?
Теперь давайте поговорим о хорошем и иначе взглянем на исходную матрицу, составленную на основе теории игр. Пусть выигрыш за отказ от секса будет варьировать – переменная г.
Уравнения смешанной стратегии для Эмми будут выглядеть так:
5?Соглашается + (r) (1 – ?Соглашается) = (r) (?Соглашается) + (0) (1 – ?Соглашается)
?Соглашается (5–2r) = r
?Соглашается = r/(5–2r)
Если мы задаем, что ?Соглашается = 0,5, то г должна быть – 1,25. Для Яна смешанная стратегия выглядит точно так же, поэтому если мы зададим г = 1,25, у пары будет секс с показателем частоты (1/2) ? (1/2) = 0,25, а это значит, что при г = 1,25 партнеры будут заниматься сексом 91 раз в год – примерно 1,8 раза в неделю.
Этот результат очень близок к среднему национальному показателю. Если мы зададим г большее значение (что будет подразумевать больший выигрыш за отказ от секса), пара будет заниматься сексом еще чаще. Например, если г = 1,53, ?Соглашается = 0,80: Эмми соглашается на секс в 80 % случаев, поэтому партнеры будут заниматься сексом (0,8) ? (0,8) ? (365) = 233 дня в году, или примерно 4 раза в неделю. Такой результат для Яна и Эмми выглядит более многообещающим.
Эти результаты позволяют предположить, что, если пара хочет часто заниматься сексом, необходимо давать выигрыш, пусть и небольшой, даже если один из партнеров отказывается от него. Если партнер говорит «нет», он должен получать положительный выигрыш. Этот вывод может показаться удивительным, но он математически обоснован.
Я знаю, что многие люди сочтут эти выкладки запутанными и сложными, но решение, которое мы получили, нельзя назвать сложным. Анализ на основе теории игр предлагает парам, которые столкнулись с угасанием желания, простую стратегию. Если они сделают так, что ответ «не сегодня» будет считаться более приемлемым, их ждет много вечеров, когда оба скажут «да». И не понадобится никакой женской «Виагры». Вполне достаточно немного чуткости.
Данный текст является ознакомительным фрагментом.