Математика безумия
Математика безумия
Любопытно: каким образом психопатия находит опору в нашем генофонде? Если это «расстройство» ведет к плохой адаптации, то почему же на протяжении длительного времени оно встречается с постоянной частотой (психопатами являются 1–2 % населения)? У Эндрю Колмана, профессора психологии из Лейстерского университета, есть такой же интригующий ответ (подозреваю, я навсегда сохраню его в своей душе после неразберихи с пересадкой в аэропорту Ньюарка).
В 1955 году состоялся дебют фильма «Восстание без причины». Никогда еще мятежную, непонятую молодежь не изображали на киноэкране с такой симпатией. Но довольно доморощенной кинокритики. Для специалистов по теории игр лучше всех в этом фильме такая сцена: Джим Старк (роль которого исполняет Джеймс Дин) и Базз Гандерсон (Кори Ален) на двух угнанных автомобилях неотвратимо несутся к краю обрыва, выясняя, кто из них круче.
Давайте на минутку посмотрим на эту сцену с точки зрения водителей, предлагает Колман. Или на ее более распространенную версию, когда два непримиримых врага мчатся навстречу друг другу, идя на лобовой таран. У каждого из них есть выбор. Они могут воспользоваться разумной, непсихопатической стратегией и свернуть в сторону, чтобы избежать столкновения. Или взять на вооружение рискованный, психопатический вариант и продолжать жать на газ. Их выбор и различные точки выигрыша представляют собой классический сценарий «почеши мне спину, и я почешу твою, — хотя, с другой стороны, может, и не почешу», который мы можем смоделировать с помощью теории игр — раздела прикладной математики, стремящегося количественно описать процесс принятия оптимального решения в ситуациях, исход которых не зависит от действий отдельных сторон, участвующих в этой ситуации. А зависит от их взаимодействия.
Таблица 3.1. Модель эволюции психопатии, основанная на теории игр.
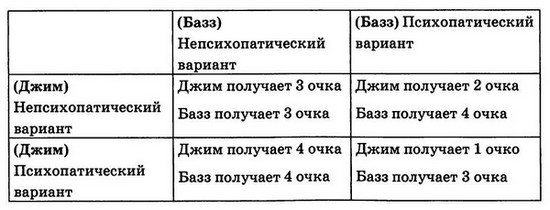
Если и Джим, и Базз выберут разумное поведение и свернут в сторону, результатом станет ничья, которая принесет второй по размеру выигрыш, и каждый получит по 3 очка. Если же оба выберут психопатической вариант поведения и решат мчаться вперед — они рискуют потерять жизнь либо получить тяжелую травму. Поэтому каждый получит минимальный выигрыш — 1 очко.
Однако вот что говорит Колман: если один из водителей, например Джим, проявит осторожность, а второй, Базз, продемонстрирует свою «крутизну», то появится разница в выигрышах. Джим проиграет и получит 2 очка. А Баззу повезет, и он получит максимальный приз — 4 очка.
Этот математический микрокосм показывает, что значит общаться с психопатами (и делать пересадку в аэропорту Ньюарка). С биологической точки зрения это работает: когда такую игру многократно повторили в лаборатории с помощью компьютерной программы, определяющей заранее установленные стратегии реагирования, произошло нечто любопытное. Если перевести выигрыш в единицы приспособленности и исходить из предпосылки о том, что игроки, получившие больше баллов, оставляют больше потомков, которые впоследствии будут использовать ту же стратегию, что и их предки, то в процессе эволюции популяции возникает стабильное равновесие. При этом доля индивидов, предпочитающих психопатическое поведение, составляет те же 1–2 %, что и доля в обществе людей с этим расстройством в реальной жизни.
Тот, кто давит на педаль газа (тот, у кого хватает для этого нервов), всегда будет побеждать — при условии, что его противник поведет себя благоразумно. На самом деле иррациональное поведение может оказаться рациональным.
В 2010 году Хидэки Охира, психолог из Университета Нагои, и его студент Такахиро Осуми доказали правильность теории Колмана для реальной жизни. Они обнаружили, что при определенных чрезвычайных обстоятельствах психопаты принимают финансовые решения лучше, чем все мы, и именно по той самой причине, которую столь элегантно продемонстрировал Колман.
Они ведут себя таким образом, который окружающим кажется иррациональным.
Для демонстрации Охира и Осуми воспользовались ультимативной игрой — парадигмой, широко используемой в нейроэкономике, которая занимается исследованиями того, как мы оцениваем выигрыши (главным образом денежные). В этой игре участвуют два игрока, которые должны решить, как им поделить выданные им деньги. Первый игрок предлагает некое решение. Второй решает, принять ли это предложение. Если второй игрок решает отвергнуть предложение, то оба противника ничего не получают. Но если второй игрок соглашается на предложенные условия, сумма делится в соответствии с ними.
Взгляните на рис. 3.1, и вы заметите нечто интересное в этой игре. Предложение, которое делает Игрок 1, может быть справедливым или несправедливым. Он может предложить поделить деньги поровну (50: 50). Или в соотношении 80: 20. Но обычно происходит следующее. Когда предложение начинает приближаться к отметке 70: 30 (в пользу Игрока 1), Игрок 2 начинает отвергать предложение.[17] В конце концов, речь идет не только о деньгах. На кону стоит принцип!
Но Охира и Осуми выяснили, что психопаты играют в эту игру совершенно иначе. Они не только демонстрируют большую готовность принять несправедливое предложение, ставя простую экономическую выгоду выше острого желания наказать «обидчика» и потешить самолюбие, но и гораздо меньше переживают из-за неравенства. Измерения кожногальванической реакции (надежного показателя стресса, основанного на автономной реакции наших потовых желез) наглядно демонстрируют различия между психопатами и остальными добровольцами. Психопаты гораздо меньше, чем представители контрольной группы, беспокоились, когда их противники жадничали. И в конце исследования они могли похвастаться большей суммой денег. Более толстая шкура обеспечивала им более толстые бумажники.
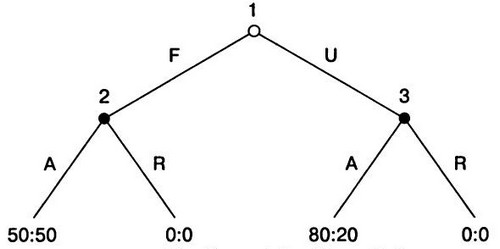
Рис. 3.1. Ультимативная игра (1 = Игрок 1; 2 = Игрок 2; F = справедливое предложение; U = несправедливое предложение; А = принятое предложение; R = отвергнутое предложение).
Охира и Осуми пришли к заключению, что иногда выгодно быть психопатом. Но в совершенно ином смысле, чем это продемонстрировал Эндрю Колман. Если Колман показал, что выгоднее бить посильнее (или, в его экспериментах, сильнее жать на газ), то Охира и Осуми продемонстрировали прямо противоположное.
Если вам нужны доказательства ценности той или иной стратегии, просто спросите у тех, кто ею пользуется.
Данный текст является ознакомительным фрагментом.