Глава 6 Взаимодействие педагога и нейропсихолога при разработке методического пособия «Состав числа»[4]

Глава 6

Взаимодействие педагога и нейропсихолога при разработке методического пособия «Состав числа»[4]

При творческом взаимодействии нейропсихологов с педагогами появляется возможность применения нейропсихологического подхода в коррекционно-развивающем обучении. Для этого необходимо создание новых блоков обучающих методик, предназначенных для облегчения усвоения учебной программы. В разработке таких дидактических материалов особенно важно участие педагогов, так как последние знают учебные программы и обладают богатым арсеналом методов по развитию познавательной активности детей. Опыт показывает, что совместная работа педагога и нейропсихолога создает условия для предупреждения школьной неуспеваемости.

Мы выбрали для разработки тему «Состав числа» по следующим причинам. Эта тема является одной из самых важных и самых сложных в программе начальной школы. Несмотря на большое количество методической литературы, касающейся данной темы, она продолжает оставаться трудной для большинства детей. Неусвоенный материал данной темы не дает ребенку возможности для успешного прохождения дальнейшей программы (автоматизация вычислительных навыков в пределах 10, сложение, вычитание чисел с переходом через десяток и т. д.).

Методическая литература по данной теме недостаточно учитывает различные трудности детей, и потому учитель не может в полной мере воплотить системный подход к освоению этого материала. Мы выделили следующие трудности детей при усвоении темы «Состав числа».

Зрительные и зрительно-пространственные:

? трудности ориентации на листе;

? трудности опознания, запоминания и актуализации пространственных структур;

? зеркальность;

? трудности работы в зрительно-насыщенном поле;

? трудности соотнесения числа с количеством. Программирование и контроль:

? неумение ориентироваться в задании, построить программу работы;

? невозможность выполнения развернутой программы, необходимость пошагового планирования извне;

? импульсивность или инактивность действий;

? трудности контроля – трудности проверки без внешних программ;

? трудности серийной организации – установления последовательности действий;

? трудности переноса способов действия.

Из анализа трудностей детей вытекают требования к построению системы методов формирования представлений о составе числа:

? необходимость условий, повышающих мотивацию к обучению (разнообразные, в том числе игровые, формы работы), повторение, не повторяясь;

? градация трудностей и организация пошагового усвоения с вынесенной программой действий, обеспечение постепенного перехода от предметного действия к выполнению заданий в уме;

? учет пространственного фактора, необходимость репрезентации количества в определенных структурах;

? учет зрительного фактора – ранжирование насыщенности зрительного поля.

Наше методическое пособие представляет собой пакет бланковых методик, построенных на основании выдвинутых требований. Здесь мы демонстрируем примеры заданий на усвоение числа «три».

Три – одна из самых простых для восприятия структур количества, ее легко определить на глаз даже маленькому ребенку. Чтобы научить ребенка считывать разнообразные структуры, мы решили представить состав числа «три» в четырех различных по пространственной ориентации вариантах. Это делает задания более интересными, дает ребенку возможность научиться анализировать зрительный материал, ориентироваться на листе, развивать зрительное восприятие и зрительно-пространственные представления.

Бланки 1, 2 (рис. 4.6.1) предполагают следующие виды заданий: обведение структур, выкладывание их из пластилина, мозаики, пуговиц, копирование структур с данного образца. Это первый уровень сложности, на котором ребенок действует по развернутой программе. На первом этапе от ребенка не требуется удержания структуры (программы) в памяти, у него есть возможность пошагового выполнения задания.

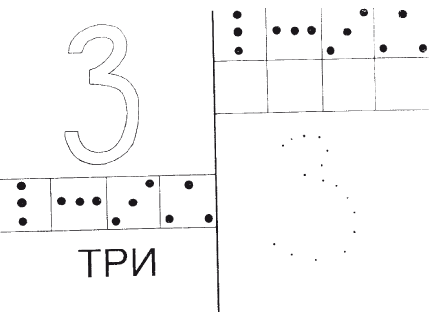
Рис. 4.6.1. Бланки 1 и 2

Бланки 3, 4, 5 предполагают узнавание и воспроизведение структур. Бланк 3 – узнавание структур точек с опорой на образец. Бланк 4 – воспроизведение структур точек по памяти (контрольное задание) (рис. 4.6.2).

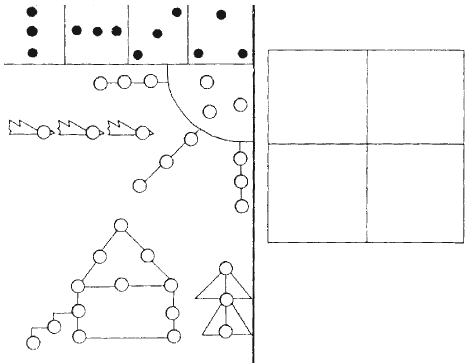
Рис. 4.6.2. Бланки 3 и 4

Бланк 5 – узнавание структур, где вместо точек выступают реальные предметы (рис. 4.6.3).

Задания такого рода предполагают удержание ребенком структуры во внутреннем плане.

На следующем уровне сложности перед ребенком ставится задача дополнения структуры до целого.

Бланк 6 (см. рис. 4.6.3) – с вынесенной программой действия. Бланки 7, 8 (рис. 4.6.4) – без нее.

Эти задания сложнее предыдущих, так как для их выполнения ребенку необходимо проанализировать предложенный рисунок, перебрать в уме возможные структуры и выбрать подходящую. В заданиях бланка 8 впервые вводится цифровое обозначение

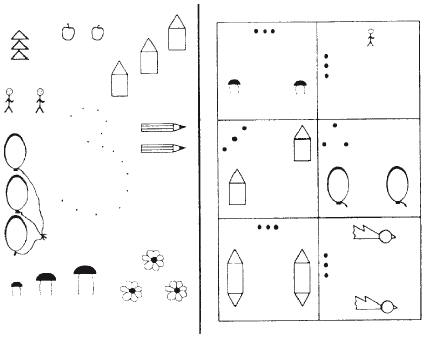
Рис. 4.6.3. Бланки 5 и 6

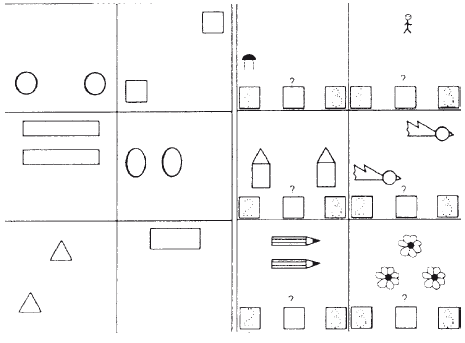
Рис. 4.6.4. Бланки 7 и 8

количества объектов без знаков действий. Оно готовит ребенка к заданиям следующего уровня сложности.

Бланк 9 (рис. 4.6.5) – контрольное задание по дополнению структуры до целого.

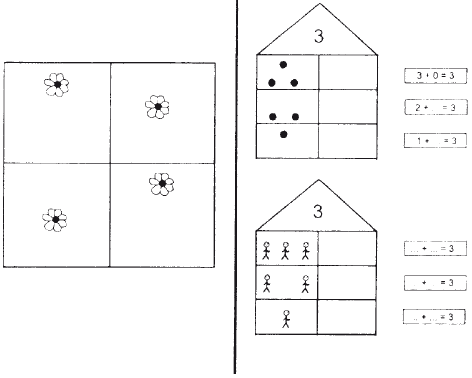
Рис. 4.6.5. Бланки 9 и 10

На бланках 10, 11, 12 даны итоговые задания. Они непосредственно выводят ребенка к активному применению полученных знаний о составе цифры «три» в арифметических действиях. На материале всех пройденных ранее видов заданий дети овладевают умением складывать и вычитать в пределах трех (рис. 4.6.6).

Данные задания апробированы при подготовке к школе детей с недостаточным развитием функций программирования и контроля и ориентировки в пространстве. Их апробация показала, что выбор материала и система предъявления адекватны возможностям детей и позволяют развивать слабые звенья высших психических функций ребенка.

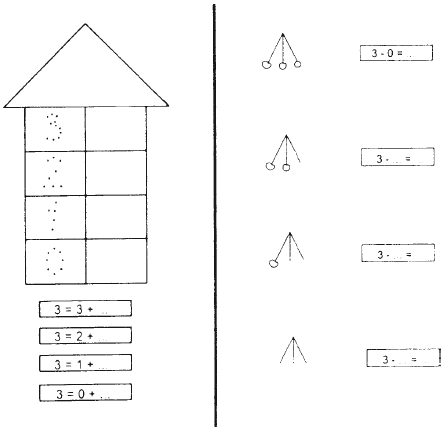
Рис. 4.6.6. Бланки 11 и 12

Данный текст является ознакомительным фрагментом.