Стратегии решения задач

Стратегии решения задач

Решение задач может быть отнесено к наиболее характерной деятельности человека.

Полья (Роlуа, 1962)

Глупо советовать человеку, столкнувшемуся с задачей, спланировать ее решение, если он понятия не имеет, как это делается. Казалось бы, что тут сложного? Нужно только разрабатывать одно за другим возможные решения и затем проверять их. А что если вы не можете придумать ни одного решения? Существует несколько стратегий, которые при правильном использовании могут помочь вам генерировать решения. Несмотря на то что ни одна отдельно взятая стратегия не может гарантировать вам универсальных решений на все случаи жизни, умение применять эти стратегии придаст направленность и уверенность вашим действиям при решении новых задач.

Шонфелд (Shoenfeld, 1979) заметил, что многие математики и ученые при решении стоящих перед ними задач прибегают к определенным стратегиям и правилам. Многие из них уверены, что если бы студенты приобрели некоторые базовые навыки, они бы решали задачи с большим успехом. Кроме того, исследователи обнаружили, что обучение, направленное на приобретение соответствующих навыков, может повысить способность человека решать возникающие задачи (напр., Klein, Weizenfeld 1978; Wickelgren, 1974). Приведенные ниже стратегии или руководства по решению задач можно рассматривать как способы планирования решения.

Анализ целей и средств

Чаще всего продвижение к цели не происходит по прямой вымощенной дороге. Если цель не может быть достигнута сразу, нередко приходится идти обходными путями или разбивать задачу на более мелкие части — так называемые подзадачи, каждая из которых имеет свою цель, или подцель.

Как и большинство стратегий решения задач, выбор и использование подцелей требует планирования. Процедура, согласно которой люди определяют подцели и используют их достижение для продвижения к основной цели, называется анализом целей и средств. Он является одним из основных, очень мощных средств решения задач. Сначала задача делится на подцели. Затем человек начинает действовать, чтобы достигнуть определенной подцели. Таким образом, с каждой отдельной победой он будет все ближе и ближе подходить к главной цели. Чтобы эта идея стала более понятной, давайте обратимся к примерам.

Первым шагом в анализе целей и средств является перечисление целей, которые можно поставить в данной задаче, и выбор наиболее перспективной из них. Предположим, что во время игры в шахматы вы поставили перед собой удачную подцель — поставить шах королю противника. Целью, естественно, является победа в игре, но для того, чтобы ее достичь, необходимо постоянно двигаться в направлении подцелей. Шах королю противника — это та ближайшая цель, в направлении которой вы продвигаетесь. Теперь вам необходимо выбрать средства для достижения данной цели — отсюда и термин анализ целей и средств. Чтобы достичь поставленной подцели, определите, какова текущая позиция ваших фигур. Затем определите разницу между той позицией, которую они занимают, и той, которой вы бы хотели достичь. Вам следует выбирать ходы, которые будут уменьшать эту разницу и позволят поставить шах королю противника. Предположим, этого нельзя добиться за один ход, тогда анализ целей и средств следует применить снова, на этот раз выбрав менее крупную подцель — возможно, это будет просто отдельный ход, направленный против какой-либо фигуры противника. Постоянное повторение этих двух процессов — выбора подцелей и сокращения расстояния до них — позволит вам продвигаться в направлении главной цели.

Любимая задача психологов, которая может служить демонстрацией анализа целей и средств, — это задача Ханойской башни. Название этой головоломке дала одна интересная легенда. Предположим, что имеются три колышка и 64 диска, каждый из которых имеет свой диаметр. Все диски нанизаны на один из колышков в порядке убывания диаметра. Для кого-то может быть удобнее представить диски в виде 64 пышек различных размеров, нанизанных одна за другой на колышек. Задача состоит в том, чтобы переместить диски с первого колышка на третий, используя средний для промежуточных действий. Правила переноса дисков заключаются в следующем: можно переносить только один диск за один раз и нельзя ставить больший диск на меньший. Легенда, связанная с задачей, гласит, что в одном монастыре вблизи Ханоя монахи заняты решением этой головоломки, а когда они закончат, настанет конец света. Даже если бы легенда оказалась правдой, у вас нет повода для беспокойства, поскольку, для того чтобы выполнить это задание, монахам понадобится примерно один триллион лет, если при этом они будут делать один ход в секунду.

Поскольку вы вряд ли собираетесь потратить столько времени на решение задачи Ханойской башни, вы можете попробовать решить ее упрощенную версию, используя только три диска. Вы легко можете приступить к решению, воспользовавшись тремя монетами различного диаметра (хорошо подойдут для этого монеты в 5 рублей, 2 рубля и 1 рубль) и тремя небольшими листочками бумаги. Сложите монеты пирамидкой на один лист бумаги так, чтобы монета наибольшего диаметра оказалась внизу, а наименьшего — наверху. Задача состоит в том, чтобы переместить монеты с первого листа бумаги на третий — при этом они должны быть расположены в том же порядке. За один прием можно брать только одну монету. Для решения задачи могут быть использованы все три листка бумаги. Записывайте все шаги, которые вы предпринимаете для решения этой задачи. Начальное и конечное положение монет показано на рис. 9.11.

Рис. 9.11. Начальное и конечное положение монет в задаче Ханойской башни. Для решения этой задачи используйте стратегию анализа целей и средств.

При анализе целей и средств задачи Ханойской башни определяется одна из очевидных подцелей — положить самую большую по диаметру монету в 5 рублей на третий лист бумаги. Этого нельзя сделать сразу, так как на ней лежат монеты в 2 рубля и 1 рубль — следовательно, надо рассмотреть вторую подцель. Она заключается в создании ситуации, когда двухрублевая монета лежит на пятирублевой. Эта подцель будет достигнута, если монета в 1 рубль будет лежать на втором листе бумаги, а монета в 5 рублей на третьем. Эта подцель не может быть достигнута, поскольку первым можно перемещать только рубль. Таким образом, последовательно рассматриваются подцели, определяющие конец каждого этапа, и действия, направленные на их достижение. Окончательное решение со всеми необходимыми ходами показано на рис. 9.12. Если вы попробуете решить эту задачу не с тремя монетами, а с четырьмя или пятью, то убедитесь, что она значительно усложнится, хотя стратегия решения останется прежней.

Рис. 9.12. Решение задачи Ханойской башни.

Обратите внимание, как достижение поставленных подцелей обеспечивает продвижение к основной цели.

Решение с конца

Анализ целей и средств является примером прямой стратегии — все планируемые действия ориентированы на приближение к подцели и, в конечном итоге, к основной цели. Иногда полезнее оказывается стратегия планирования операций решения с конца, которые обеспечивают движение от конечной цели назад — к текущему или исходному положению. Простейшим примером такой стратегии может служить игра в обожаемые детьми лабиринты, нарисованные на бумаге, которые нужно проходить с помощью карандаша.

Многие из этих лабиринтов содержат несколько возможных путей, отходящих от начальной точки, и среди них только один верный путь, который приведет в конец лабиринта к заветной цели. Даже маленькие дети понимают, что они смогут ускорить решение такой задачки-лабиринта, если пойдут в обратном направлении, начав движение с конечной точки и прорисовывая путь к началу лабиринта. Пример такого лабиринта приведен на рис. 9.13.

Стратегия решения с конца очень удобна, если от конечной цели ведет меньше путей, чем из исходного положения. Разумеется, эта стратегия может быть применена не только для прохождения лабиринтов. Рассмотрим такую задачу: «Площадь, которую покрывают водяные лилии на одном из озер, удваивается каждые двадцать четыре часа. С того момента, как появилась первая лилия, до того, когда лилии полностью покрыли поверхность озера, прошло шестьдесят дней. Когда озеро было покрыто наполовину?» (Fixx, 1978, р. 50).

Единственным путем решения этой задачи является применение стратегии решения с конца. Можете ли вы решить ее, пользуясь этой подсказкой? Если озеро полностью было покрыто лилиями на 60-й день, а площадь, которую покрывают лилии, удваивалась каждые сутки, какая часть озера была закрыта в 59-й день? Ответ: половина. Таким образом, пользуясь обратным ходом, мы легко решили эту задачу. Прямая стратегия решения этой задачи наверняка завела бы нас в тупик.

Иногда оказывается эффективной комбинация прямой стратегии и стратегии решения с конца. Если вы столкнулись с геометрической или тригонометрической задачей на доказательство, то, вполне вероятно, прибегнув к комбинации этих двух стратегий, вы успешно с ней справитесь. Вы можете начать с конечного выражения, преобразуя его до какой-то определенной стадии, затем последовательно переходить от преобразования этого выражения к преобразованию исходного выражения и наоборот — до тех пор, пока они не совпадут на каком-то промежуточном этапе.

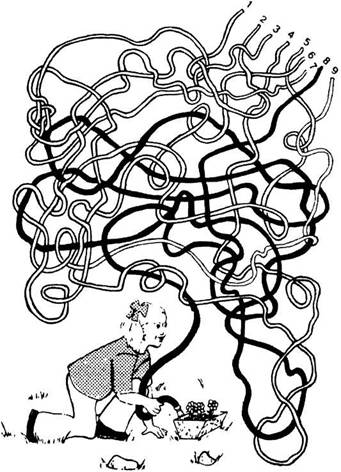
Рис. 9.13. Стратегия решения с конца удобна, когда из конечной точки ведет меньше путей, чем из исходного положения.

Упрощение

Вы все обдумываете и обдумываете свою задачу; попробуйте упростить ее… Довели ли вы ее до максимально возможного упрощения, до той ясности, которая наталкивает на мысли?

Полья (Роlуа, 1962)

Задачи, вызывающие затруднения при решении чаще всего сложны по структуре. Хороший способ справиться с такой задачей — это упростить ее настолько, насколько возможно. Нередко удачно выбранная форма наглядного представления задачи сама способствует ее упрощению, поскольку позволяет «увидеть» эффективный путь решения.

Предположим, вы столкнулись с классической задачей «кошка на дереве». Согласно устоявшемуся мнению, кошки могут карабкаться вверх по деревьям, но не могут спускаться. (На самом деле в этом утверждении не больше правды, чем в том, что слоны боятся мышей.) Предположим, вам надо снять кошку с ветки, расположенной на высоте 10 футов. В вашем распоряжении имеется единственная лестница длиной 6 футов. Для того чтобы лестница была надежно установлена, ее основание должно находиться на расстоянии трех футов от ствола. Дотянетесь ли вы до кошки?

Лучший путь к решению этой (и не только этой) задачи — графически изобразить исходные данные. Условия задачи графически показаны на рис. 9.14. Как только информация представлена в виде чертежа, ее можно воспринимать как простую геометрическую задачу: найти гипотенузу прямоугольного треугольника, если его катеты равны 10 и 3 футам. Такая формулировка задачи предполагает, что вы воспользуетесь своими знаниями о том, как вычисляются длины сторон треугольников. Факт остается фактом: когда для решения задачи требуется определенный уровень образования — его ничем не заменишь.

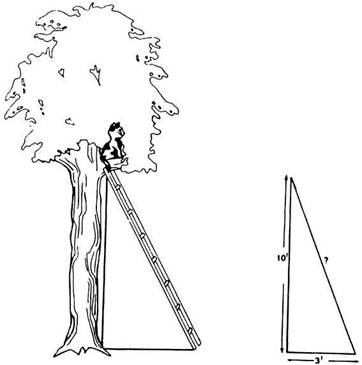
Рис. 9.14. Задача «кошка на дереве».

Если исходные данные представить в виде рисунка, задача превращается в простую геометрическую задачу.

Формула для нахождения гипотенузы треугольника имеет вид:

а² + Ь² = с².

Подставляя соответствующие значения в это уравнение, получим:

10² + 3² = с²

100 + 9 = с²

109 = с²

?109 = c

с= 10,4

Таким образом, для того чтобы достать до ветки, нужна лестница длиной 10,4 фута. Но постойте, может, попробовать перерисовать задачу, используя условие, что для спасения кошки в вашем распоряжении имеется только шестифутовая лестница? На рис. 9.15 приведена несколько другая графическая интерпретация этой задачи.

Может быть использована та же формула, но теперь неизвестной величиной является не гипотенуза, а один из катетов прямоугольного треугольника.

Рис. 9.15. Задачу «кошка на дереве» можно переформулировать таким образом: как высоко от земли располагается конец лестницы в 6 футов, если ее основание отставить на 3 фута от ствола?

Тогда и ответ получится другой.

Изменяя формулу, получим:

а² + Ь² = с²

а² = с²-Ь²

а² = 6²-3²

а² = 36-9

а² = 27

a = ?27

a = 5,2

Таким образом, верхняя планка лестницы коснется ствола дерева на высоте 5,2 фута над землей. Сможете ли вы достать кошку? Нарисуйте себя на верхней ступеньке. Если вы выше 5 футов, то без труда дотянетесь до кошки, стоя на последней или даже предпоследней ступеньке. На самом деле вам даже не придется тянуться.

Упрощение является хорошей стратегией для решения абстрактных задач, сложных или содержащих информацию, не относящуюся к поиску решения. Часто стратегия упрощения работает рука об руку с выбором оптимальной формы представления задачи, поскольку именно удачное наглядное представление может существенно упростить задачу.

Обобщение и специализация

Иногда, столкнувшись с задачей, оказывается полезно рассмотреть ее как частный случай целого класса аналогичных задач (обобщение); или, наоборот, как специальный случай (специализация).

Чаще всего стратегии обобщения и специализации уместны при представлении задачи в форме древовидной диаграммы. Большинство целей в этом случае может одновременно классифицироваться как подчиненные для вышестоящей категории и главные для нижестоящей. Рассмотрим пример, проясняющий сказанное. Предположим, что перед вами как дизайнером мебели стоит задача разработки проекта специального удобного стула для чтения. Что бы вы предприняли для решения этой задачи?

Как вы уже, по-видимому, поняли — это пример нечетко поставленной задачи. Самая большая сложность состоит в том, чтобы выбрать: какой из нескольких возможных вариантов стульев наиболее подходит поставленной цели? Воспользуйтесь древовидной диаграммой, чтобы классифицировать стулья вообще и стулья для чтения в частности. Таких диаграмм можно построить множество; один из возможных вариантов приведен на рис. 9.16.

Рис. 9.16. Одна из возможных древовидных диаграмм задачи проектирования стула для чтения.

Надеюсь, что вы сами поработали над этой задачей и построили свою диаграмму. Как можно видеть из рис. 9.16, восприятие «стула для чтения» как отдельного элемента категории «стулья» помогает учесть при рассмотрении проекта как общие качества стульев, так и уникальные качества «стульев для чтения». Таким образом, процесс обобщения и/или специализации позволит вам взглянуть на задачу как в широкой перспективе, так и в узкой.

Случайный поиск и метод проб и ошибок

Вспомните, что структура задачи включает в себя исходное положение и цель, а также пути решения, ведущие от исходного положения к цели. Одной из стратегий поиска возможных путей решения является случайный поиск. Хотя такой подход не выглядит серьезной стратегией решения задачи, а кажется скорее псевдостратегией, в некоторых случаях он оказывается весьма полезным. Если задача имеет небольшое число возможных путей решения, то случайный поиск приведет к цели в кратчайший срок. Совершенно случайный поиск означал бы отсутствие систематического порядка рассмотрения вариантов и возможность повтора уже рассмотренных решении. Поэтому более предпочтительной стратегией является систематический поиск методом проб и ошибок по всему пространству задачи (содержащему пути решения, цель и исходное положение). Лучше всего применять метод проб и ошибок к решению четко поставленных задач, имеющих конечное число возможных путей решения. Применение этого метода хорошо подходит при решении коротких анаграмм. Например, переставьте следующие буквы так, чтобы получилось слово:

БДУ

Поскольку возможны только шесть вариантов последовательностей расположения этих букв (БДУ, ДБУ, УБД, УДБ, ДУБ, БУД), то можно без труда найти решение простым перебором вариантов. Если бы вы воспользовались чисто случайным поиском, то не хранили бы в памяти уже рассмотренные варианты и повторяли бы некоторые из них по несколько раз, пока не наткнулись бы на верное решение. Систематический поиск методом «проб и ошибок» почти всегда имеет преимущества перед случайным поиском — однако эти преимущества менее заметны при большом числе возможных вариантов решения.

Обе стратегии — метод проб и ошибок и случайный поиск — плохо работают, когда возрастает количество путей решения задачи из-за роста числа возможных комбинаций. Часто бывает полезным разбить задачу на части и воспользоваться методом проб и ошибок для решения более мелких подзадач.

Правила

Некоторые типы задач строятся по определенным правилам — например, задачи на последовательности. Как только будут установлены принципы построения такой задачи, можно считать ее решенной. В области математики и физики большинство задач построено по определенным правилам. Хороший способ обнаружить заложенную в задаче закономерность — это попробовать отыскать повторяющиеся фрагменты в данных или подцелях. Такого сорта задачи, требующие поиска закономерности, часто используются в тестах интеллекта.

Продолжите следующую запись:

АББАВВВАГГГГА

Это пример задачи на простейшую последовательность. Следующими шестью буквами будут ДДДДДА. В таких задачах часто встречаются определенные повторяющиеся фрагменты. Чтобы их обнаружить, посчитайте число повторяющихся символов, внимательно просмотрите значительные по длине участки последовательности и постарайтесь отыскать закономерность — при этом попробуйте воспользоваться простейшими операциями сложения и вычитания. Это вовсе не тривиальная задача! Расшифровка военных донесений противника во время Второй мировой войны явилась важнейшим фактором, внесшим вклад в нашу победу. Соединенные Штаты Америки и Великобритания привлекли к работе большое количество профессиональных шифровальщиков, в чью обязанность входило отыскать ключ к шифрам военных донесений Германии и Японии.

Представим на минуту, что в космическом пространстве существует разумная жизнь и что эти разумные существа тоже интересуются нами. Как они дадут нам знать, что они существуют? Некоторые ученые, фантасты да и многие простые люди считают, что они могут дать знать о своем присутствии, послав сообщения. Никто не рассчитывает, что эти сообщения будут на английском или китайском языках, языке островов Самоа или на каком-нибудь другом земном языке. Они отправят сообщение на своем родном языке или, если они не имеют языка, другими доступными им средствами. Как же мы, земляне, распознаем это сообщение? Военное ведомство США уверено, что если мы когда-нибудь получим сообщения из других миров, то они будут построены по правилам определенной «грамматики» и содержать повторяющиеся фрагменты. Может, это покажется странным, но военные исследуют космическое пространство, что бы найти излучения с повторяющимися фрагментами. И до тех пор пока они ничего не нашли, мы можем продолжать верить, что являемся самыми разумными существами во Вселенной (или, что более разумные существа не желают быть обнаруженными, не могут или не хотят вступать с нами в контакт).

Подсказки

Подсказки — это дополнительная информация, которая сообщается человеку после того, как он начал работать над задачей. Часто подсказка содержит важные дополнительные сведения, необходимые для принятия решения. Иногда она может потребовать от вас изменить намеченный путь решения задачи. Распространенным примером использования подсказок служит детская игра в «холодно-горячо». В помещении спрятан какой-то предмет. Ребенок, который «водит», бродит по комнате, а другие дети кричат «теплее», если он приближается к спрятанному предмету, и «холоднее», если он от него удаляется. В этой ситуации «водящему» нужно продолжать двигаться небольшими шажками в одном направлении, пока дети кричат подсказку «теплее», и попытаться незначительно изменить направление, когда они подсказывают «холоднее». Исследования воздействия подсказок на процесс принятия решений показали, что общие слова-подсказки типа «подумай о других способах использования предметов» не способствуют поиску решения (Duncan, 1961). Чем определеннее и точнее подсказка, тем больше пользы можно из нее извлечь.

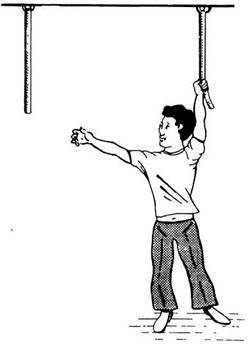
Рис. 9.17. Задача о двух веревках. Как ухватить две веревки одновременно? (Maier, 1930)

Одной из любимых задач психологов является так называемая задача о двух веревках. Представьте себе, что вы входите в комнату, в которой с потолка свешиваются две веревки. Они расположены достаточно далеко друг от друга, чтобы вы могли одновременно дотянуться до обеих, но ваша задача состоит именно в этом. Эта ситуация изображена на рис. 9.17.

Наилучшим решением этой задачи является раскачивание одной из веревок с предварительно привязанным к ее свободному концу тяжелым предметом — так, чтобы человек, перед которым возникла такая задача, смог ухватить конец качающейся веревки, когда она приближается к нему. После того как исследователи дают подсказку, предложив отгадывающему представить, что он случайно задел веревку и привел ее в колебательное движение, он чаще всего быстро справляется с задачей, правда, лишь немногие при этом отчетливо осознают, что воспользовались подсказкой (Maier, 1931).

Чтобы выяснить, как люди пользуются подсказками, было проведено экспериментальное исследование, в ходе которого участники должны были заучить пары слов — так чтобы, когда экспериментатор произнесет одно слово, они были готовы назвать его пару (это называется парно-ассоциативное заучивание). Одной из таких заученных пар слов была пара «свеча-коробка». После заучивания всего перечня словесных пар тестируемым была предложена задача Дункера (Duncker, 1945) о свече, которую требуется прикрепить к стене при помощи коробки (см. рис. 1.1). Помогла ли эта подсказка решить задачу? В большинстве случаев, после того как экспериментатор посоветовал тестируемым вспомнить пары заученных слов, они справились с этой задачей гораздо легче (Weisberg, Bransford, Franks, 1978). Они непроизвольно воспользовались этой подсказкой для решения задачи — скорее всего, так и не распознав ее. Проведенное недавно исследование подтвердило такой эффект и в случаях с другими задачами (Perfetto, Bransford & Franks, 1983). В целом, можно считать, что подсказка полезна только тогда, когда занятый решением задачи человек воспринимает ее как один из возможных путей решения.

Люди, успешно решающие задачи, как правило, ищут подсказки. Сбор дополнительной информации можно рассматривать как такой поиск. Практически всегда полезно получить максимум возможной информации по интересующей вас задаче. Дополнительные данные помогут реорганизовать пространство задачи и укажут направление, в котором проще искать пути решения.

Метод деления пополам

Метод деления пополам является прекрасной стратегией поиска, когда заранее не существует причин для выбора путей решения из последовательно организованного множества. Предположим, что из-за засорения водопровода у вас на кухне из крана не течет вода. Засорение произошло где-то между местом подсоединения ваших труб к магистральному водопроводу и кухонным краном. Как вы найдете место засорения в трубе, сделав при этом минимальное количество отверстий?

В этом случае решение (место образования пробки) надо искать по всей длине трубы. Наилучшим способом решения такой задачи является метод деления пополам. Поскольку задача предполагает, что вы будете сверлить трубу в каждом выбранном месте, надо максимально эффективно выбирать эти места. Начните с середины пути между отводом от главной трубы и кухонным краном. Если вы обнаружите, что до этого места вода свободно поступает, то место засорения трубы находится где-то между этой точкой и вашей раковиной. После этого разбейте пополам уже этот участок. Если вода течет и здесь, то вам станет ясно, что пробка находится где-то ближе к раковине, и вам следует разбить пополам оставшийся участок.

Допустим, в результате первой попытки вы обнаружили, что вода не доходит до просверленного места. Тогда засорение должно быть между главной трубой и этой точкой. Следующий поиск вы должны вести именно на этом участке. Таким способом вы будете продолжать поиск, пока место засорения трубопровода не будет найдено. Это очень удобный метод решения подобных задач — например, при решении задачи поиска места разрыва электропроводки в вашем доме или автомобиле.

Вы можете воспользоваться методом деления пополам в игре под названием «Угадай возраст» (я ее сама придумала). Ваши друзья могут «прикинуться» людьми любого возраста. Вы можете угадать возраст любого из них от 0 до 100 не более чем за семь высказанных догадок. Как это проделать? Начните с возраста, лежащего посередине между 0 и 100 — т. е. с 50. Игрок должен будет ответить, старше или моложе 50 лет задуманный возраст. Ответ будет «старше» или «моложе». Положим, он отвечает, что «моложе». Какой возраст вы назовете следующим? Вам следует выбрать возраст посередине между 0 и 50 — т. е. 25. Предположим, теперь он ответит «старше». Ваша третья догадка должна лежать посередине между 25 и 50. Поскольку мы имеем дело только с целыми числами, то следующим должно быть названо число 38. Если теперь он ответит «моложе», вы называете 32, т. е. число, лежащее посередине между 25 и 38. Если ответ «старше», вы выбираете 35 (середина между 32 и 38). Если ответ «моложе», вы называете 33. Теперь вы точно знаете, что игрок загадал себе возраст либо 33, либо 34. Таким образом, любой возраст может быть определен не более чем за семь высказанных предположений. Попробуйте проделать это с некоторыми из своих друзей. Это будет для вас хорошей практикой использования стратегии деления пополам. Вспоминайте об этой стратегии в ситуациях, когда задача имеет несколько возможных равновероятных решений.

Мозговая атака

Лучший способ иметь хорошие идеи — это иметь много идей.

Линус Паулинг

Мозговая атака — это весело. Первоначально она была предложена Осборном (Osborn, 1963) как метод группового решения задачи, но оказалась полезной и для индивидуальной работы над задачей. Мозговая атака нужна для поиска дополнительных путей решения и может быть призвана в помощь всегда, когда возникают трудности с их нахождением. Ее целью является выработка как можно большего числа решений. Она призвана подтолкнуть людей, занятых решением задачи, к выдвижению самых безумных, невероятных и фантастических идей. Все эти идеи заносятся в список — причем независимо от того, насколько глупыми они кажутся. Принцип, заложенный в основу этой стратегии, заключается в том, что чем больше количество высказанных идей, тем больше вероятность, что, по крайней мере одна из них окажется удачной. Чтобы поощрить творческую силу воображения, правила этой стратегии исключают всякую критику и высмеивание идей, даже если они совершенно бредовые. Вынесение решения о ценности идей переносится на последующие стадии работы над задачей. Иногда различные идеи частично комбинируются в целях усовершенствования. Мозговая атака может быть предпринята большой или маленькой группой людей, а также в одиночку. После проведения мозговой атаки перечень возможных решений должен быть тщательно изучен, чтобы найти решения, выполненные с учетом наложенных на данную задачу ограничений — чаще всего финансовых, временных и этических.

Мозговая атака была эффективно использована одним из производителей пищевых продуктов, который столкнулся с задачей улучшения упаковки картофельных чипсов. Работников корпорации попросили придумать способ упаковки — лучше всех тех, какие они когда-нибудь видели. Один из них предложил упаковывать мокрые чипсы и уверял, что это будет наилучшим решением. Когда вы пытаетесь сложить в пакетик сухие чипсы, они крошатся и плохо укладываются, но если смочить их перед упаковкой, то можно использовать пакеты меньше размером и облегчить их наполнение — пустот в таком пакете будет меньше. Следуя этому совету, работники попробовали сначала смочить чипсы, а затем наполнять ими пакеты. Результат оказался плачевным — чипсы высыхали и превращались в безвкусные крошки. Но эта идея в конце концов привела к широко популярным картофельным чипсам, которые аккуратно, один на другой, уложены в коробку. Эти чипсы изготавливаются из жидкого картофельного пюре, которое запекается в специальных формах. Таким образом, непродуманная и не очень хорошая затея (смачивание картофельных чипсов) вылилась в довольно удачное решение.

Противоречие

Лучшие решения многих задач нередко должны сочетать противоположные свойства. Например, рассмотрим задачу безупречной коробки для пиццы — такой, которая сохраняет пиццу горячей, но при этом не позволяет скапливаться внутри пару, чтобы корочка не становилась влажной. Здесь присутствуют два противоречивых условия — хранить пиццу закрытой, чтобы она оставалась горячей, и не давать конденсироваться пару и увлажнять корочку. Когда вы в следующий раз закажете пиццу, изучите коробку, в которой ее доставили. Большинство коробок для пиццы представляет собой компромисс между двумя упомянутыми выше условиями — крышка закрыта, чтобы сохранить пиццу горячей, но при этом она имеет маленькие вентиляционные отверстия, позволяющие некоторому количеству пара выходить наружу. Это пример компромиссного решения. Пицца остывает быстрее, поскольку через вентиляционные отверстия проникает холодный воздух, но при этом корочка на ней лишь слегка увлажняется, так как благодаря наличию отверстий количество конденсирующейся влаги ограничено.

Одним из соблазнов при решении любой задачи, включающей в себя противоречие, является отказ от компромисса — т. е. хочется придумать такое решение, которое удовлетворяет всем заданным условиям задачи. Это, конечно, хорошо, но как этого добиться? Что касается задачи упаковки пиццы, то Вальдман и Цуриков (цит. по: Raia, 1994) разработали коробку с «впадинками» (рельефными углублениями) на дне, которые заставляют пар конденсироваться внизу, а не на корочке пиццы — при этом удержанный под пиццей горячий воздух создает дополнительную теплоизоляцию.

Вальдман и Цуриков разработали компьютерную программу, предлагающую бескомпромиссные способы удовлетворения противоречивых условий при решении любых задач. Они просмотрели файлы Патентного бюро США и обнаружили свыше 200 основных принципов решения широкого круга задач, которые могут быть использованы как по отдельности, так и в комбинации друг с другом. Программа начинается с запроса четкого определения типа задачи, которая решается. Это своего рода поиск основных принципов (например, необходимость изоляции и исключение конденсата, безотносительно к пицце). Варианты решений поступают из банка данных, составленного на базе решения других задач, включавших противоречия того же типа — т. е. вызывается нужный алгоритм (те шаги, которые были использованы для решения) теории изобретательного решения задачи. И хотя реклама этого доступного пользователям программного продукта сулит фантастические успехи, необходимо проведение дополнительных исследований беспристрастными специалистами — и вот тогда мы по праву оценим его эффективность. Воспользовавшись основной идеей, мы сможем создать оптимальное решение любой задачи, а затем, по-видимому, начнем думать, как же приспособить ее к конкретным условиям.

Приведем другой пример задачи, включающей в себя противоречия. Рассмотрим задачу сбора помидоров. Механические сборщики томатов сами по себе дешевые и довольно быстрые, но они мнут плоды. Компромиссным решением было бы применение мягких прокладок в устройстве механической сборки или замедление этого процесса, чтобы снизить количество раздавленных помидоров. Но кардинальным правилом теории изобретательного решения задачи является отказ от компромиссов. Лучшей идеей, которая не потребует снижать скорость работы механического сборщика, оставляя при этом плоды целыми, является выращивание помидоров с более толстой кожицей, которая не позволит им быть раздавленными неуклюжими и быстро перемещающимися механическими сборщиками (The Cognition and Technology Group at Vanderbilt, 1993). Итак, очевидное противоречие (быстрый сбор томатов с помощью машин без их повреждения) было разрешено без компромисса.

Переформулировка задачи

Переформулировка задачи оказывается наиболее полезной стратегией при решении нечетко поставленных задач. В четко поставленных задачах цель обычно определена однозначно в недвусмысленных терминах, которые практически не оставляют свободного пространства для переформулировки — хотя, как показано ранее, четко поставленная задача, по-видимому, могла бы фактически иметь много возможных модификаций, если бы мы были в состоянии изменить ее формулировку и цель. Эта стратегия была описана выше.

Рассмотрим задачу, с которой сталкивается фактически каждый взрослый человек, с которым мне приходилось встречаться. «Как накопить деньги?» Многочисленные семьи по всему миру, пытаясь решить эту задачу, совершают покупки на оптовых рынках, едят бутерброды с арахисовым маслом и проводят субботние вечера дома. Предположим, вы переформулировали задачу, и она стала звучать так: «Как мне стать богаче?» Дополнительные решения этой задачи теперь будут включать в себя поиски более высокооплачиваемой работы, переезд на квартиру подешевле, поиск богатого мужа (жены), инвестиции в высокодоходное предприятие, выигрыш в ирландском тотализаторе и т. д. Как только вы сталкиваетесь с нечетко поставленной задачей, постарайтесь переформулировать цель. Очень часто это оказывается весьма действенным способом, поскольку другая цель будет иметь и другие пути решения. Чем больше в вашем распоряжении окажется путей решения задачи, тем с большей вероятностью вы достигнете цели.

Аналогии и метафоры

Едва ли мы сможем вообразить абсолютно новую задачу, не похожую и не связанную ни с одной ранее решенной; но если такая задача могла бы существовать, она была бы неразрешимой. Действительно, при решении задачи нам всегда следует извлекать уроки из ранее решенных задач, используя их результаты, методы и опыт, приобретенный при их решении.

Полья (Роlуа, 1945, р. 92)

Гик и Холиок (Gick & Holyoak, 1980) задали вопрос: «Откуда возникают новые идеи?» Многие ученые и математики отвечают, что их идеи или решения задач приходят из осознания аналогий и метафор, извлеченных из различных академических дисциплин (Hadamard, 1954). На деле же оказывается, что большинство общих выводов сделано при обнаружении подобия (аналогий и метафор) между двумя или более ситуациями. Подобно подсказке, аналогия должна восприниматься как составная часть решаемой задачи, в соответствии с которой ее и надо преобразовать.

Решим следующую задачу.

Маленькая страна попала под жестокую диктатуру. Диктатор правил страной, находясь за мощными стенами крепости. Крепость была расположена в центре страны и окружена деревнями и фермами. От нее отходило по радиусам множество дорог, подобно спицам на колесе. И тут появился храбрец-генерал. Он собрал большую армию на границе и поклялся захватить крепость и освободить страну от диктатора. Генерал знал, что если вся его армия одновременно пойдет в атаку, крепость будет захвачена. Когда его войска, готовые к атаке, уже выстроились в начале одной из дорог, ведущих к крепости, вдруг прискакал разведчик и вручил генералу сообщение, которое внесло заминку. Безжалостный диктатор заминировал все дороги. Мины были установлены таким образом, что небольшие группы людей могли спокойно преодолевать их, поскольку диктатору необходимо было иметь воинов и слуг, постоянно передвигающихся из крепости и обратно. Однако при прохождении целого войска сработают взрыватели. Это не только разрушит дорогу и сделает ее непроходимой, но и послужит поводом диктатору в отместку разорить соседние деревни. Поэтому прямая атака на крепость всем войском казалась невозможной (Gick & Holyoak, 1980, p. 351).

Чтобы помочь вам справиться с этой задачей, я сделаю подсказку. Решение аналогично одному из рассмотренных ранее в этой главе, хотя контекст совершенно другой. Прервитесь на несколько минут и попытайтесь поработать над задачей. Вспомните о задачах, рассмотренных ранее. Может, вам будет проще найти решение, если вы нарисуете схему.

Решение этой задачи аналогично решению, которое было принято в случае наличия неоперабельной опухоли в желудке. В той ситуации (Duncker, 1945) наилучшим решением было облучение всего тела направленными со всех сторон слабыми лучами с тем» чтобы они фокусировались в месте нахождения опухоли. Подобным образом армия могла бы быть разбита на несколько небольших групп, которые атаковали бы крепость со всех сторон. Осознали ли вы, что эти задачи похожи и могут решаться одинаково?

Гордон (Gordon, 1961), основатель группы под названием «Синектика», составил руководство пользования аналогиями при решении задач. Термин «Синектика» заимствован из греческого языка. Он означает соединение вместе различных и не имеющих видимых связей элементов. Гордон предложил рассматривать четыре типа аналогий, которые встречаются в задачах.

1. Личная аналогия.

Если вы хотите разобраться в сложном явлении, представьте себя составной частью этого явления. Например, если вы хотите понять молекулярное строение смеси, представьте себя молекулой. Как бы вы повели себя? Как поступили бы другие молекулы, к которым вы намерены прицепиться? Старайтесь не искать научного объяснения, а действительно ощутите себя молекулой, беспорядочно толкающейся в смеси. Может, вы увидите с этой точки зрения те неуловимые связи, которые были закрыты от вас как от ученого.

Использование личных аналогий особенно эффективно при решении широкого круга конфликтных ситуаций. Если бы каждая из конфликтующих сторон могла взглянуть на задачу и ее цель с точки зрения противоположной стороны, то, вероятно, возникли бы новые решения. Обе стороны могут обнаружить общие интересы и, воспользовавшись этим, найти приемлемый для всех выход (Bernstein, 1995; Fisher & Ury, 1991).

2. Прямая аналогия.

Сопоставьте задачу, над которой вы работаете, с рядом задач из совсем других областей. Как указывает Гордон (Gordon, 1961), этот метод был использован Александром Грехэмом Беллом: «Меня осенило: ведь на самом деле хрящи человеческих ушей слишком массивны по сравнению с нежной тонкой мембраной, которая управляет ими, и если такая тонкая мембрана может заставить двигаться относительно громоздкие хрящи, то почему бы моей более толстой и плотной мембране не заставить двигаться стальную пластинку. Так был придуман телефон».

Поистине плодородным источником аналогий является биология, где с момента зарождения первых форм жизни в процессе эволюции было решено множество задач. Когда члены «Синектики» столкнулись с необходимостью придумать эффективный способ закупоривания бутылок с клеем или лаком для ногтей, то они воспользовались биологической аналогией смыкания прямой кишки. Действительно, это решение сработало превосходно. (Вы можете поразмыслить об этом, когда будете пользоваться бутылкой клея ЛеПейдж.)

3. Символическая аналогия.

Эта стратегия решения задач требует зрительного воображения. Ее цель — оторваться от ограничений, накладываемых словами или математическими символами. У студентов, которые подключили воображение для создания визуальной картины в задаче с опухолью и крепостью, самопроизвольно возникло понимание того, что эти две задачи являются аналогичными. Если вы пытаетесь создать четкий зрительный образ задачи, то можете увидеть и решение, просвечивающее сквозь этот образ.

4. Фантастическая аналогия.

Какое решение приходит вам на ум в ваших самых безумных мечтах? Например, вы можете вообразить двух маленьких насекомых, которые будут автоматически застегивать вашу куртку, или гусеницу-шелкопряда, которая начнет быстро прясть шелк, чтобы вы не замерзли при резком похолодании. Это примеры фантастических аналогий. Как и в случае мозговой атаки, фантастические аналогии могут выражаться в безумных, далеких от реальности идеях, которые, весьма вероятно, затем будут преобразованы в практические и выполнимые решения.

Хотя совершенно ясно, что аналогии оказывают существенную помощь в решении задач, большинству людей редко удается самостоятельно выявить потенциальную аналогию (VanLehn, 1989). Если вы в состоянии изобразить внутренние связи, как в предыдущей задаче, или установить основные правила, как это было в задачах с противоречиями, то, вероятнее всего, вы уясните себе структуру решаемой задачи и найдете подходящую аналогию.

Консультация специалиста

Если у вас не получается сразу, пробуйте снова и снова. Затем отступите. Что толку ощущать себя полным болваном.

У. С. Филдс (цит. по: Teger, 1979, р. XIV)

В жизни часто случается, что мы не можем решить задачу в одиночку. Иногда лучшим способом решения задачи является привлечение специалиста. Люди обращаются к бухгалтерам для решения вопросов платежей, к адвокатам по правовым вопросам, к врачам при возникновении проблем со здоровьем. Мы выбираем чиновников, которые будут решать задачи нашей страны, а ведение войны поручаем военным специалистам. Эти люди стали высококлассными экспертами в своей области благодаря приобретению соответствующих знаний и неоднократному применению этих знаний для решения задач на практике. Поэтому часто консультации специалистов становятся отличным способом решения задачи. Их опыт и знания, превышающие ваши собственные, позволят решать задачи, относящиеся к их специальности, намного эффективнее, чем это сделает новичок. Если вы решили проконсультироваться у специалиста, то задача приобретает вид: а) как узнать, является ли данный человек специалистом, и б) как выбрать, к какому из специалистов следует обратиться. Решением этих вопросов дело не закончится. Вам нужно быть уверенными, что привлеченный к работе специалист имеет в руках все факты и рассмотрел все возможные альтернативы. Внимательно выслушайте его анализ возможного риска и альтернативных путей, но окончательное решение — за вами. Специалист — это только помощь в решении задачи, но не само решение. Некоторые советы по выбору нужного специалиста вы можете найти у Карлсона (Carlson, 1995) или в разделе о компетенции в главе 4.

Крок. Авторы Билл Речин и Дон Уайлдер

Выбор наилучшей стратегии

Всего в этой главе было представлено 13 различных стратегий, способных оказать помощь при решении задач. Как узнать, какой из них воспользоваться, столкнувшись с конкретной задачей? Важно постоянно помнить, что эти стратегии не являются взаимоисключающими. Часто оказывается полезной их комбинация. Выбор наилучшей стратегии или комбинации стратегий зависит от сути задачи. Например, когда вы сдаете экзамен, вас могут просто попросить покинуть аудиторию, если вдруг обнаружится, что в качестве «консультанта» вы выбрали конспект своего соседа.

Описывая каждую из стратегий, я пыталась дать некоторые советы по ее использованию. В целом же более высокий уровень знаний — «стратегия выбора стратегии» — включает в себя следующее:

1. Если задача является нечетко поставленной, представьте ее цель и условие в нескольких различных формулировках.

2. Если задача имеет несколько (но небольшое количество) возможных решений, имеет смысл воспользоваться методом проб и ошибок.

3. Если задача слишком сложна, попытайтесь применить упрощение, анализ целей и средств, обобщение и специализацию.

4. Если от конечной цели отходит меньше путей, чем от исходного положения, примените стратегию решения с конца.

5. Если у вас есть возможность собрать дополнительную информацию, сделайте это. Поищите подсказки, посоветуйтесь со специалистом.

6. Если исходные данные задачи представляют собой упорядоченную последовательность или массив либо задача имеет равновероятные альтернативные решения, попробуйте воспользоваться методом деления пополам или отыскать правило, по которому построен массив данных.

7. Если количество возможных путей решения задачи слишком мало, то, для того чтобы генерировать дополнительные решения, примените мозговую атаку.

8. Проектные и инженерные задачи чаще других задач требуют поиска решений, которые должны будут удовлетворять самым противоречивым условиям.

9. Использование аналогий и метафор, консультация специалиста — все это наиболее широко применяемые стратегии для решения задач любого типа. Надо быть всегда готовым использовать визуализацию и выполнить осмысленный поиск аналогий с целью подбора аналогичного решения.

10. Помните, что это лишь советы по поиску решений задач. Наилучший способ стать высококлассным специалистом по решению задач — это решить как можно больше задач.