Прогнозы на основе объединения информации

Прогнозы на основе объединения информации

Хосе всегда хотел стать артистом. Поэтому он планирует продать все свое имущество и отправиться в Нью-Йорк делать карьеру. Предположим, и вам, и Хосе известно, что лишь 4 % людей, мечтающих стать актерами, добиваются в Нью-Йорке профессионального успеха. Это значение является базовым уровнем; оно основано на информации, известной еще до того, как мы получим какую-либо конкретную информацию о Хосе. Давайте остановимся и обдумаем эту цифру — базовый уровень. Она говорит о том, что очень немногие из людей, мечтающих стать актерами, становятся профессионалами в этой области. Другими словами, шансы на успех низкие. Предположим, что у вас нет никакой дополнительной информации о Хосе. Как бы вы оценили его шансы на успех? Если вы ответили 4 %, вы совершенно правы! В отсутствие какой-либо другой информации используйте базовый уровень.

Хосе считает, что ему не стоит беспокоиться: дело в том, что 75 % тех, кто преуспел на актерском поприще, имеют кудрявые волосы, а также хорошо поют и рассказывают анекдоты. Поскольку у Хосе кудрявые волосы, он хорошо поет и уморительно рассказывает анекдоты, то он уверен, что скоро будет рассылать поклонникам свои глянцевые фотографии размером 8 х 10. Значение второй вероятности называется вторичным; оно отражает специфическую информацию о характеристиках Хосе и желательного исхода. Мы используем эти два значения вероятностей для того, чтобы решить, обоснован ли оптимизм Хосе. Каковы его точные шансы на успех? Не забывайте, что вероятности лежат в диапазоне от 0 до 1, причем 0 означает, что Хосе точно потерпит неудачу и ему придется возвратиться домой, а 1 означает, что он совершенно точно добьется успеха на Бродвее. Теперь остановитесь и оцените субъективную вероятность его успеха.

Можете ли вы предложить способ определения объективной вероятности успеха? Чтобы найти объективную вероятность, вам потребуется знать еще одно число, про которое часто забывают, — процент тех, кто терпит неудачу, несмотря на то, что обладает характеристиками, связанными с успехом (в данном случае, кудрявыми волосами и умением петь, танцевать и шутить). Очень немногие люди понимают, что при оценке вероятности успеха необходимо учитывать эту величину. Для краткости изложения я буду обозначать характеристики, связанные с успехом (кудрявые волосы и умение петь и шутить), просто «кудрявые волосы», а отсутствие этих качеств — «нет кудрявых волос». Предположим, что 50 % потерпевших неудачу обладают этими качествами. В таком контексте для расчета вероятностей тоже можно использовать древовидные диаграммы. Давайте начнем с начала и рассмотрим все возможные исходы. В данном случае Хосе либо добьется успеха, либо потерпит неудачу, поэтому мы назовем первые ветви «успех» и «неудача». Как и прежде, мы будем надписывать вероятность каждого события вдоль соответствующей ветви.

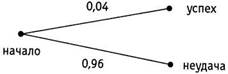
Отметим, что эти две вероятности (0,04 и 0,96) в сумме равны 1,0, поскольку других возможных исходов нет. Один из этих исходов обязательно осуществится, поэтому сумма их вероятностей равна 1,0, что указывает на достоверность.

Хосе знает, что у 75 % из тех, кто добивается успеха, бывают кудрявые волосы. В этом примере мы пытаемся найти вероятность определенного исхода (успеха) при условии, что у нас уже имеется некоторая информация, касающаяся вероятности этого исхода. Давайте добавим новые ветви, исходящие из узлов «успех» и «неудача». В этом примере существуют четыре различных исхода: успех при наличии кудрявых волос, успех при отсутствии кудрявых волос, неудача при наличии кудрявых волос и неудача при отсутствии кудрявых волос. Эти четыре исхода показаны на следующей диаграмме:

Отметим, что поскольку 75 % (0,75) добившихся успеха имеют кудрявые волосы, а 25 % (0,25) не обладают этой характеристикой, то сумма вероятностей событий, исходящих из одного узла, должна равняться единице. Точно так же 50 % потерпевших неудачу имеют кудрявые волосы, а 50 % неудачников не обладают этим качеством. Поскольку мы учитываем всех неудачников, то сумма этих вероятностей также должна равняться единице.

После того как диаграмма нарисована, подсчитать объективную вероятность успеха Хосе уже совсем просто. Как и раньше, чтобы найти вероятность какого-либо исхода, надо перемножить вероятности вдоль ведущей к нему ветви. В данном случае мы перемножим вероятности вдоль каждой из ветвей диаграммы и представим результаты в виде таблицы:

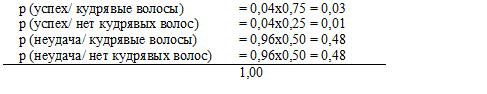
Из таблицы видно, что общая доля людей, обладающих кудрявыми волосами, равна 0,03+ 0,48 = 0,51.

Чтобы определить истинные шансы Хосе на успех, нам следует разделить долю людей, добившихся успеха и обладающих кудрявыми волосами (0,03), на общую долю тех, кто имеет кудрявые волосы (0,03 + 0,48 = 0,51). Мы пытаемся прогнозировать успех Хосе на основе знания того факта, что у него кудрявые волосы, а некоторая часть людей с кудрявыми волосами добивается успеха. Какую часть всех людей с кудрявыми волосами (0,51) составляют те, кто добился успеха (0,03)?

Доля добившихся успеха с кудрявыми волосами / Общая доля людей с кудрявыми волосами = 0,03 / (0,03 + 0,48) = 0,06

Таким образом, шансы Хосе на успех на 50 % выше (6 % против 3 %), чем у любого неизвестного, желающего стать артистом, но все равно они очень низкие. Наличие информации о том, что он обладает некоторыми качествами, связанными с успехом, привело к некоторому увеличению вероятности его успеха по сравнению с базовым уровнем, но это увеличение очень незначительно.

Возможно, вам покажется проще следить за логикой этих расчетов, если вы сведете всю информацию в таблицу:

Вы не удивлены, что его шансы на успех оказались столь низкими, несмотря на то, что последующая или вторичная вероятность имела такое высокое значение (75 %)? Большинство людей оказывается удивлено таким результатом. Столь слабые шансы Хосе стать артистом объясняются тем, что в целом на этом поприще добивается успеха очень небольшое количество желающих. Полученное Хосе значение вероятности было близко к априорному, или базовому, уровню успеха для всех начинающих артистов. Поскольку в целом очень немногим артистам удается добиться успеха, Хосе, как и любой другой будущий артист, имеет низкие шансы на успех. Исследования показали, что вообще большинство людей склонно к переоценке шансов на успех при низких базовых уровнях и к их недооценке при высоких базовых уровнях. В предыдущем примере, касавшемся Эдит, у нас была лишь информация о базовом уровне, на которой основывался процесс прогнозирования. В этом примере у нас есть информация о Хосе, которая позволила нам предсказать его шансы на успех, превышающие базовый уровень, хотя из-за общей низкой доли успеха кандидатов в актеры в целом это повышение было незначительным.

Тем читателям, которые предпочитают мыслить пространственными категориями, я предлагаю представить себе большую группу людей, 4 % из которых являются добившимися успеха артистами, а 96 % — не являются таковыми. Эта группа изображена на рис. 7.5. Четверо из 100 нарисованных человечков улыбаются — так изображены добившиеся успеха актеры. Если у вас нет другой информации для прогнозирования успеха Хосе, то вам придется воспользоваться этим базовым уровнем и предсказать ему 4 % шансов на успех.

Рис. 7.5. Наглядное изображение 4 %-го уровня успеха. Заметьте, что 4 % лиц улыбаются.

Теперь давайте учтем дополнительную информацию: 75 % тех, кто добился успеха, имеют кудрявые волосы, а из тех, кто потерпел неудачу, кудрявыми волосами обладают лишь 50 %. Эта информация сочетается с информацией о базовом уровне. Результат изображен на рис. 7.6, где добившимся успеха и неудачникам пририсованы кудрявые волосы. Из четырех улыбающихся человечков трое (75 %) обладают кудрявыми волосами, а из 96 хмурых человечков кудрявые волосы у 48 (50 %).

Анализируя эти цифры, легко заметить, что наши математические действия заключались в том, чтобы определить долю улыбающихся человечков с кудрявыми волосами по отношению ко всем человечкам с кудрявыми волосами, а затем использовать то, что мы знаем о Хосе, для предсказания его шансов на успех. Графически это доля (или часть), которую составляют три улыбающихся кудрявых человечка по отношению к оставшемуся 51 кудрявому человечку:

3/51=0,06

Обобщая; получим следующую схему для расчета вероятности исхода при условии, что у вас имеется информация, касающаяся этой вероятности.

1. Нарисуйте полную древовидную диаграмму, указав информацию о базовом уровне (например, успеха или неудачи), в первой группе узлов. Вторичной информацией воспользуйтесь при изображении второй группы узлов

2. Составьте таблицу, где все различные сочетания базовой и вторичной информации представлены в виде строк.

3. Перемножьте вероятности вдоль каждой из ветвей диаграммы и запишите результаты в строках таблицы.

4. Составьте дробь, в которой значение вероятности интересующей вас ветви (например, успех при наличии кудрявых волос) будет числителем, а сумма этого значения и значения вероятности из другой ветви, содержащей то же условие (например, неудача при наличии кудрявых волос), будет знаменателем.

5. Проверьте ответ. Имеет ли он смысл? Следует ли ожидать, как в приведенном примере, что вероятность успеха должна быть выше базового уровня, потому что у нас имеется информация, которая связана с успехом? (Если бы мы знали, что Хосе обладает некоторым качеством, которое связано с неудачей, то мы бы предсказали, что его шансы на успех будут ниже базового уровня, но при изначально низком базовом уровне они уменьшатся ненамного.)

Существует большое количество заболеваний, базовый уровень вероятности заболеть которыми невелик для группы населения. Результаты медицинских тестов следует интерпретировать с учетом соответствующего базового уровня каждой болезни. Медицина, как и большинство других дисциплин, является вероятностной наукой; тем не менее, очень немногие врачи получают подготовку по теории вероятностей. Неумение применять информацию о базовых уровнях может привести к неверным диагнозам. Игнорирование базового уровня является распространенной ошибкой, допускаемой при размышлении об исходах вероятностных событий. Дреман (Dreman, 1979) суммирует результаты большого количества исследований на эту тему следующим образом: «Тенденция к недооценке или полному игнорированию известных вероятностей при принятии решений, несомненно, является самым серьезным недостатком интуитивного мышления» (цит. по: Myers, 1995, р. 331). Последствия подобных постоянных ошибок и когнитивных предубеждений играют серьезную роль не только в экономике, управлении и капиталовложениях, но практически в любой области, где приходится принимать решения, связанные с вероятностью.

Рис. 7.6. Наглядное изображение относительной доли добившихся успеха актеров и неудачников, обладающих такими же характеристиками, как Хосе. Эти характеристики изображены в виде кудрявых волос.

Нерегрессивные суждения

Гарри недавно поступил в Государственный арбузолитейный университет. Средний балл всех студентов этого университета (СБ) равен 2,8. Гарри — новичок и еще не сдавал экзаменов. Хотя у вас нет никакой конкретной информации о Гарри, как вы думаете, каков будет его средний балл? Прекратите чтение и попытайтесь угадать его средний балл.

После первых экзаменов в середине семестра Гарри получил средний балл 3,8. При наличии этой новой информации как вы теперь оцените СБ Гарри, который он получит в конце учебного года? Большинство людей на первый вопрос сразу отвечает 2,8, т. е. называют средний балл всех студентов арбузолитейного университета. Это правильный ответ, поскольку, не имея другой информации, лучше всего заключить, что средний балл любого из студентов этого университета близок к общему среднему баллу. На второй вопрос большинство людей отвечает 3,8. К сожалению, это не самый лучший ответ. Хотя и верно, что человек, получающий высокие оценки на экзаменах в середине семестра, как правило, получает высокие оценки на экзаменах за весь семестр, все же эти оценки не совпадают в точности. Обычно человек, получивший очень высокий по какой-либо шкале результат, в следующий раз получает результаты ближе к средним. Следовательно, средний балл Гарри в конце учебного года, скорее всего, будет меньше, чем 3,8, и больше, чем 2,8. (Точный прогноз среднего балла можно вычислить математически, но эти расчеты выходят за рамки данной книги.) Эта идея сложна для понимания, поскольку большинство людей находит, что она противоречит интуиции, и это действительно так.

Полезно рассмотреть пример из области спорта. Вспомните своих любимых спортсменов. Хотя они иногда выступают совершенно блестяще, чаще всего их результат близок к среднему. В конце концов, невозможно всегда сбивать все кегли или выбивать 1000 очков. Любителям спорта известно явление, которое носит название «синдром второго года». После выдающихся успехов в течение первого года выступлений на следующий год звезда обычно начинает показывать результаты, которые ближе к среднему уровню. Еще один пример, который может помочь прояснить эту концепцию, — это часто используемый пример о росте отцов и сыновей. Как правило, сыновья отцов очень высокого роста имеют рост ближе к среднему (хотя все же выше среднего). Это явление носит название регрессии к среднему значению. (Среднее значение вычисляется путем сложения всех интересующих вас значений и деления на число этих значений.)

Выше в этой главе я говорила о законах случая. Никто не может точно предсказать рост конкретного человека. Но в целом — т. е. если обследовать очень много отцов высокого роста, то окажется, что у большинства из их сыновей рост регрессирует к среднему значению. Таким образом, как и было сказано выше, знание законов вероятности помогает нам лучше прогнозировать, но точные прогнозы будут получаться не всегда. Важно понимать эту концепцию, имея дело с вероятностными событиями.

Канеман и Тверски (Kahneman Tversky, 1973) изучали последствия, возникающие вследствие того, что специалисты не понимают явления регрессии к среднему. Израильские летные инструкторы хвалили курсантов, когда они успешно выполняли сложные фигуры пилотажа и маневры, и критиковали плохие полеты. С учетом того, что вы только что узнали о регрессии к среднему значению, понятно, что должно произойти после того, как пилот отлично справился с заданием? Последующие полеты, вероятно, окажутся ближе к среднему уровню, потому что класс пилотажа регрессировал к среднему. И наоборот, чего следует ожидать после очень плохого полета? Опять-таки, последующие должны быть ближе к среднему уровню — в данном случае это означает, что они станут лучше, хотя могут все равно остаться ниже среднего уровня. Инструкторы не понимали явления регрессии к среднему значению, поэтому пришли к неверному выводу о том, что похвалы приводят к ухудшению результатов, а критика — к улучшению.

Давайте рассмотрим еще один пример регрессии к среднему значению. Это явление носит повсеместный характер, но очень немногие люди знают о нем. Предположим, что вы узнали о группе самопомощи для людей, дети которых очень плохо себя ведут. (Такие группы действительно существуют.) Большинство родителей обращается в такие группы тогда, когда их дети ведут себя особенно плохо. После нескольких недель посещения группы многие родители сообщают, что поведение их ребенка стало лучше. Можно ли сделать вывод, что занятия в группе помогли родителям научиться управлять поведением своих детей? Вспомните о регрессии к среднему значению! Если родители поступили в группу, когда поведение их ребенка было особенно плохим, то что бы они ни делали — даже если бы они не делали ничего, — все равно поведение ребенка, скорее всего, должно регрессировать к среднему по условной шкале поведения уровню. Мы можем прогнозировать не ангельское или хотя бы нормальное, т. е. среднее поведение, а только некоторое улучшение или изменение поведения в сторону среднего уровня. Поскольку это статистический прогноз, иногда он может оказаться неверным, но в среднем (в достаточно протяженном интервале времени) мы будем правы. Поэтому нельзя сделать никаких выводов об эффективности занятий в группе самопомощи, если не провести эксперимент того типа, который был описан в главе 6. Нужно будет случайным образом распределить детей и семьи по группам самопомощи и контрольным группам, а затем определить, будут ли дети из групп самопомощи вести себя значительно лучше, чем дети из контрольной группы, на которых не оказывали никакого специального воздействия. Для того чтобы заключить, что такие группы помогают улучшить поведение ребенка, мы должны иметь возможность случайным образом распределить семьи по группам. Если вы начнете искать в жизни случаи регрессии к среднему значению, то удивитесь, какое количество событий можно объяснить именно «движением к среднему значению», а не какими-либо другими причинами.