Правильность и структура составляющих

Чтобы рассмотреть функционирование языковых грамматик в аспекте грамматической правильности, представим себе ситуацию с корзиной, наполненной до краев небольшими полосками бумаги. На каждой из полосок написано какое-нибудь слово английского языка. Здесь же находится и наш друг Атико, представитель одного из племен юго-восточной Эфиопии. Атико не разговаривает на английском языке и не понимает его. Каждый раз он вытягивает из корзины по десять полосок бумаги, а затем раскладывает их перед собой слева направо в той последовательности, в которой они были извлечены из корзины. Его задача состоит в том, чтобы решить, является ли полученная последовательность из десяти слов грамматически правильным предложением английского языка. Мы можем помогать ему, только подсказывая систему правил, с помощью которых он должен вынести свое решение.

При таком подходе грамматика представляет собой процедуру принятия решений, которая разбивает совокупность всех возможных последовательностей слов английского языка на множество грамматически правильных последовательностей и множество грамматически неправильных последовательностей. Так как Атико не знает правил английского языка, правила должны быть заданы ему эксплицитно, делая заключение, он не может полагаться на свои интуитивные представления. Далее, если система правил составляет адекватную (в смысле определения правильности) грамматику, то каждая последовательность слов, которая была с ее помощью определена как правильное предложение, должна быть сочтена таковой и носителем английского языка. И наоборот, все без исключения последовательности слов, попавшие в множество неправильных последовательностей, носитель языка тоже должен идентифицировать как неправильные. Мы вкратце представляем вам систему правил, используемую трансформационными лингвистами. Эта система станет более понятной, если мы вначале рассмотрим структуру составляющих. Возьмем в качестве примера предложение:

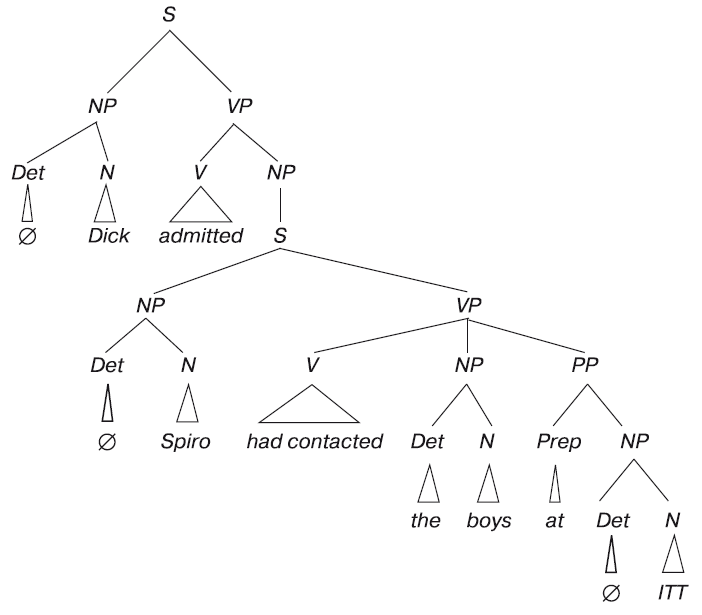
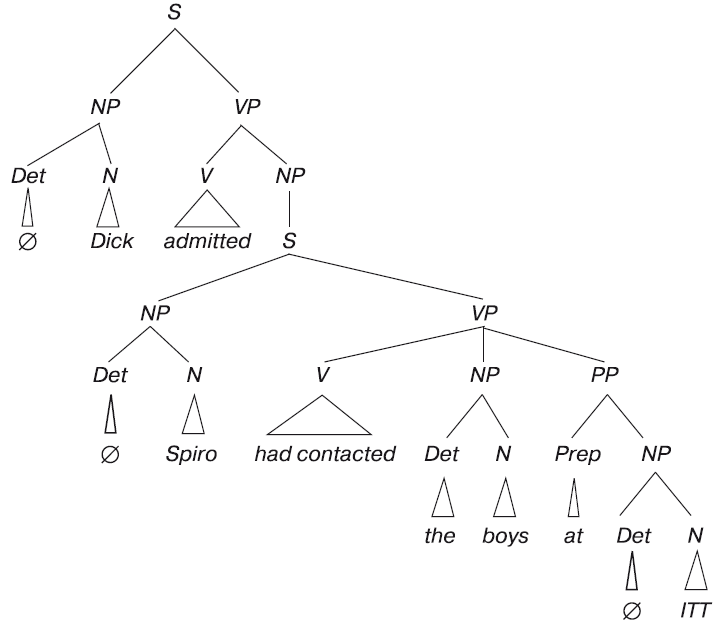
(1) Dick admitted Spiro had contacted the boys at ITT. (Дик предположил, что Спиро установил контакт с этими ребятами из ITT.)

Написанное выше предложение я идентифицирую как правильное, и то же самое скажете вы и любой другой носитель английского языка. А теперь спросите себя, можете ли вы определить внутреннюю структуру данного предложения. Например, есть ли у вас интуитивное представление, что слова the и boys («этими» и «ребятами») каким-то образом объединены, а слова boys и at («ребятами» и «из») – нет? Или, опять же, что можно неким образом объединить слова had и contacted («установил» и «контакт»), но не слова contacted и the («контакт» и «этими»)? Носитель языка ответит утвердительно на оба эти вопроса. Мы можем, основываясь на наших интуитивных представлениях относительно внутренней структуры, исследовать это предложение и дальше, чтобы определить, каким образом его отдельные слова группируются вместе, образуя единицы более высокого уровня.

После того как мы просмотрим предложение один раз, мы можем сделать это снова, объединяя уже выделенные единицы в составляющие еще более высокого уровня. Например, составляющие had contacted и the boys («установил контакт» и «этими ребятами») образуют такую единицу, a Spiro и had contacted («Спиро» и «установил контакт») – нет. Данную процедуру можно повторять и дальше. Представления носителей языка, вроде нас с вами, относительно структуры составляющих являются последовательными. Еще раз повторим, что последовательность мы понимаем в том смысле, что, если вы увидите это предложение снова через десять лет, ваши суждения относительно его структуры не изменятся. И при этом ваши суждения будут совпадать с суждениями любых других носителей данного языка. В рамках трансформационной грамматики этот вид интуитивных знаний представлен в виде структуры дерева.

Есть простая процедура, позволяющая перейти от наших интуитивных представлений к «структуре дерева»: слова, которые я интуитивно объединяю вместе, приписываются одному и тому же узлу в структуре дерева. Например, слова the и boys («этими» и «ребятами») мы интуитивно объединяем в начальную группу, и, соответственно, репрезентируя их в виде дерева, создадим структуру:

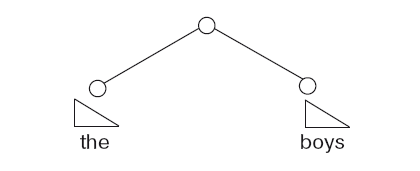
В структуре дерева узлы (обозначаемые на рисунке кружками) носят названия, которые соответствуют представляемым частям речи. Например, S — предложение, NP – именное словосочетание, VP — глагольное словосочетание, N – имя (существительное, местоимение), V — глагол, Det – определение, РР — предложное словосочетание, Prep — предлог и т. д. Таким образом, репрезентация словосочетания «этими ребятами» в виде дерева примет следующий вид

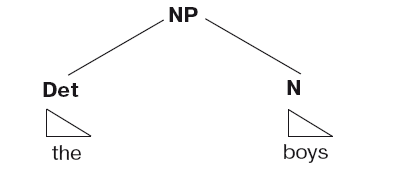
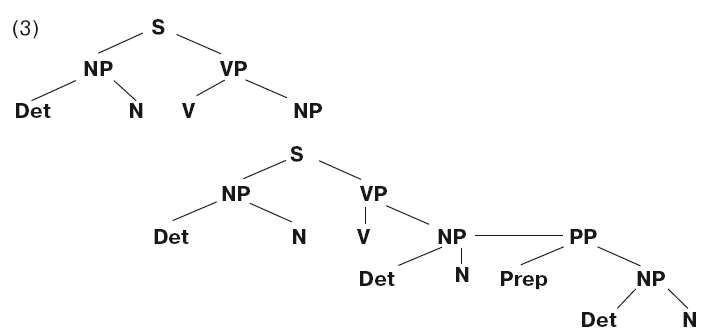
Структура дерева (2) представляет наши интуитивные представления относительно внутренней структуры предложения (1).

Теперь, познакомившись с процедурой перевода интуитивных представлений в структуру дерева, вы можете просмотреть эту структуру и проверить, совпали ли наши с вами интуитивные представления. Например, слова had contacted the boys at ITT («установил контакт с этими ребятами из ITT») образуют составляющую ( VP), а слова Spiro и had contacted («Спиро» и «установил контакт») – нет. В структуре дерева это находит отражение в том, что первая последовательность исключительным образом составляет отдельный узел (говоря «исключительным образом», мы имеем в виду, что данный узел содержит только эти слова и никаких других), но нет узла, который исключительным образом содержал бы слова «Спиро» и «установил контакт».

Выше мы говорили, что грамматика представляет собой систему правил. На что еще похожа система правил, которые определяют формирование структуры дерева? Чтобы ответить на этот вопрос более понятным для вас образом, нам придется дать краткое описание формальных или логических систем.

Формальные системы

Формальные системы включают три компонента:[55]

• словарь;

• набор аксиом;

• набор правил формирования, или вывода.

Наиболее важные (для наших целей) понятия формальной системы можно продемонстрировать на примере следующей системы, назовем ее «Простая». [56]

Символ _ означает, что символы, находящиеся слева от него, могут быть замещены (быть переписаны как) символами, находящимися справа от него.

Теперь давайте посмотрим, как действует эта система. Метаправило (правило для правил) формальных систем данного класса требует, чтобы мы обосновывали каждое утверждение, которое делаем внутри системы. Есть два возможных способа обоснования: либо на основе того, что мы ранее заявили как аксиому, либо на основе подстановки, совершаемой в предыдущей строке в соответствии с правилами вывода. Поскольку у нас еще нет ни одной строки, в первой мы должны написать аксиому системы.

Теперь исследуем только что написанную строку и проверим, нет ли в ней символов, соответствующих левой части одного из правил вывода. В ней находится единственный символ , и этот символ действительно появляется в левой части обоих правил вывода системы «Простая». Теперь мы можем выбрать одно из правил и написать следующую строку.

Мы можем повторить процедуру, проверив, нет ли в последней строке символов, которые содержатся в левой части одного из правил вывода. Внутри нашей системы эта процедура может повторяться сколь угодно долго до тех пор, пока мы выбираем правило вывода а.[57]

Допустим, вы выбрали правило вывода а еще дважды.

Что произойдет, если мы теперь выберем правило б?

Если мы теперь проверим последнюю строку последовательности, мы не обнаружим в ней символов, которые встречались бы в левой части какого-либо из правил вывода, так что процедура подошла к концу. Результат данной процедуры – совокупность всех строк, от первой до последней, – называется выводом. Последняя строка вывода называется теоремой системы и считается доказанной для данной системы. Наконец, последовательность элементов, входящих в словарь системы, считается правильно сформированной, если она представляет собой доказанную теорему данной системы. Рассматривая систему в целом, мы можем видеть, что последовательность элементов будет считаться правильно сформированной (в рамках данной системы) только в том случае, если ее вывод осуществляется из аксиомы с помощью правил вывода, до тех пор пока не будет получена строка, не содержащая символов, которые встречались бы в левой части какого-либо из правил вывода, то есть теорема. Если мы возьмем всю совокупность теорем системы, мы получим множество правильно сформированных последовательностей элементов данной системы.

Теперь мы хотели бы более отчетливо пояснить параллели между системой «Простая» и системами естественного языка. Первая задача, которая стоит перед нами как лингвистами, это определить множество правильно сформированных последовательностей элементов системы естественного языка, для которого мы пытаемся сконструировать грамматику. Затем, используя «Простую» в качестве модели, мы попытаемся определить систему правил, которая позволила бы нам представить в виде теорем все последовательности слов данного языка, которые носители языка считают правильно сформированными. Если мы сделаем это, можно будет считать, что мы сумели решить вопрос принадлежности к множеству.

Механизмы принадлежности к множеству и вопросы структуры составляющих

Давайте посмотрим, какой могла бы быть система правил естественного языка.

Метаправило данной системы совпадает с метаправилом предыдущей системы «Простая» – каждая строка вывода может либо представлять собой аксиому, либо должна быть выводима из предыдущей строки на основе правил вывода. Используя ту же процедуру что и в случае системы «Простая», получаем.

Перейти от выводов к репрезентации в виде дерева очень просто: надо вернуться к первой строке вывода и начать читать его последовательно, строка за строкой. В каждой строке, применяя одно из правил вывода, заменяем один символ на другой символ (символы), а остальные символы просто копируем из предыдущей строки. Эти символы не несут новой информации и, следовательно, являются избыточными. Мы ликвидируем избыточность, стирая, или удаляя, в каждой следующей строке вывода все символы, на которые не повлияло приложенное правило вывода. Если мы выполним данную операцию с несколькими первыми строками вывода, то получим следующую фигуру:

Теперь вернемся к первой строке вывода и, последовательно спускаясь вниз, соединим каждый символ из одной строки с тем символом или символами, на которые мы заменили их в последующей строке. В результате первые несколько строк приобретут вид

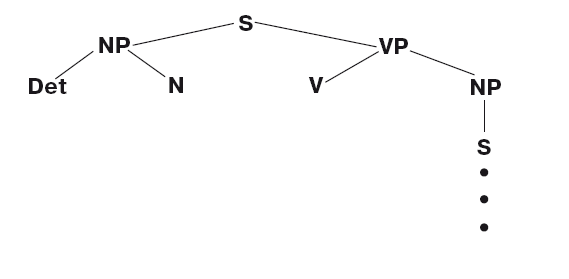
А когда мы применим эти две процедуры ко всему выводу целиком, мы получим репрезентацию в виде дерева.

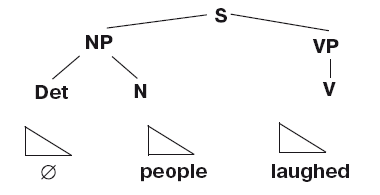
Эта структура дерева идентична обсуждавшейся выше структуре дерева (2), если не считать того, что в ней отсутствуют самые нижние узлы, которые содержали смысловые слова предложения. Чтобы добавить их, нам необходим расширенный словарь (лексикон). Лексикон предоставляет в наше распоряжение все смысловые слова английского языка вместе с определенной дополнительной информацией. Например, слова перечислены в лексиконе с указанием того места, которое они могут занять в структуре дерева. Глагол «предположил» можно поместить в узел V, если с этим узлом сочетается узел NP, как в структуре дерева (2),[58] но его нельзя поместить в структуру дерева под узлом У, если этот узел ни с чем не сочетается, как следующем случае.

Такого рода информация, помещенная в лексиконе, предотвращает появление неправильных последовательностей вроде: [59]

* People admit. (Люди предполагают.)

*Dick laughed Spiro had contacted the boys at ITT. (Дик смеялся, что Спиро установил контакт с этими ребятами из ITT.)

Для существительных лексикон содержит информацию о том, с какими глаголами их можно использовать, чтобы избежать появления неправильных последовательностей, например, таких:[60]

*The wall laughed. (Степа смеялась.)

*The wall admitted Spiro had contacted the boys at ITT. (Степа предположила, что Спиро установил контакт с этими ребятами из ITT.)

В общем, лексикон содержит достаточно информации, чтобы установить зависимости между глаголами и соответствующими им именными группами. Если мы имеем лексикон, все, что нам еще нужно, – это правила подстановки, с помощью которых можно проверить соответствие информации из лексикона структуре дерева и, если они не противоречат друг другу, поместить слово в нужный узел. Если мы проделаем всю операцию подстановки для дерева (3), мы получим в результате дерево (2), которое, для удобства, и воспроизводим здесь еще раз.

Итак, что же нам дает структура «Глубинная»? Во-первых, она репрезентирует интуитивные представления о структуре составляющих. Каким образом? Проверим правила вывода этой структуры. Возьмем, например, правило г: РР ? Prep NP

Это выражение можно интерпретировать не просто как правило вывода, мы можем рассматривать его как правило структуры составляющих. В этом смысле оно гласит, что предложная группа состоит из предлога и именной группы. В более общем виде: каждое правило вывода определяет, какие символы, находящиеся справа от стрелки, являются составляющими, которые исчерпывающим образом определяются символами, находящимися слева от стрелки, и затем замещают их.

Во-вторых, система «Глубинная» является первым приближением к системе, которая репрезентирует наши интуитивные представления о том, что такое «правильно сформулированный», то есть что такое предложение английского языка. В данном случае к ним относятся все доказанные теоремы системы «Глубинная». Как нам узнать правильный ли это ответ? В принципе, мы можем запустить систему «Глубинная», собрать все доказанные таким образом теоремы и сравнить это множество с множеством предложений, которые носители языка определили как правильные. Практически, однако, мы можем показать, что система «Глубинная» не дает исчерпывающего ответа на этот вопрос, если найдем хотя бы одно правильно сформулированное предложение, которое не являлось бы доказанной теоремой в данной системе. Ниже мы приводим пример такого предложения:

(4) The boys at ITT were admitted by Dick to have been contacted by Spiro. (Диком было предположено, что Спиро был налажен контакт с этими ребятами из ITT.)

Как нам определить, является ли предложение (4) теоремой системы «Глубинная»? Во-первых, мы должны просмотреть его и, опираясь на наши интуиции, определить, как слова в нем объединяются в первичные группы и какой, следовательно, будет его структура дерева. Например, мы можем отметить, что слово at («из») образует со словом ITT такую начальную группу, а слово boys («ребята») со словом at и слово ITT со словом were («было») – нет. Просматривая предложение второй раз, мы обнаружим, что составляющие were admitted и Dick («было предложено» и «Диком») образуют группу, в то время как составляющие at ITT и to have been contacted («из ITT» и «был налажен контакт») – нет. Осуществив такой систематический просмотр предложения, мы можем представить наши интуитивные представления в виде структуры дерева (5).

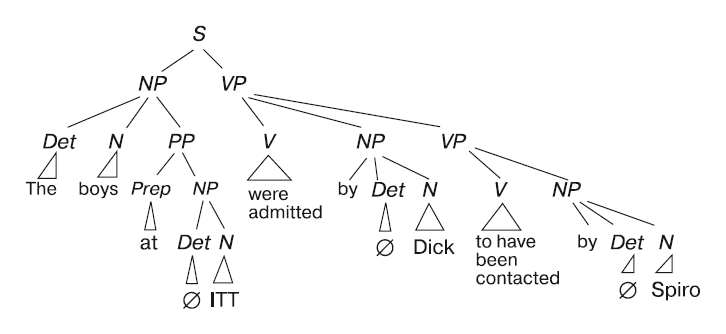
Наши интуитивные знания, представленные в виде дерева, содержат несколько любопытных моментов. Например, мы видим на рисунке составляющую, в которую входят предлог «by», Det и N, и вместе они исчерпывающе образуют узел NP. Это доказывает, что система «Глубинная» только частично отвечает на вопрос о принадлежности к множеству. Каким образом доказывает? Проверим в системе «Глубинная» правила, которые определяют, какие составляющие исчерпывающе входят в узел NP, то есть правило вывода б. Поскольку в данной системе нет правила вывода, обусловливающего возможность замещения NP на by+Det+N, мы видим, что в ней невозможен вывод (а следовательно, и доказанная теорема), в котором узел NP непосредственно включал бы элемент «by». Чтобы могла появиться подобная конфигурация, для нее должно быть соответствующее правило формирования. И, таким образом, мы можем заключить, что нашлась как минимум одна правильная последовательность слов, не учтенная системой «Глубинная». Но прежде чем мы попытаемся добавить сюда другую систему или дополнительные правила вывода, мы хотели бы поговорить об интуитивных представлениях, связанных с синонимией.