Нейронные сети

Нейронные сети

 Упрощенное понимание работы нейрона легло в основу компьютерного моделирования процессов, напоминающих работу мозга. Такие модели называются нейронными сетями.

 Нейронная сеть — это совокупность моделей нейронов, объединенных между собой большим числом связей. Нейрон имеет связи, по которым к нему поступает информация. Все входы — взвешенные, то есть каждому входу присвоен весовой коэффициент. Сигналы, попадающие на нейрон, суммируются и через функцию входа-выхода подаются на выход нейрона. Топология соединений нейронов зависит от типа сети.

 По структуре связей нейронные сети делятся на два больших класса: однослойные и многослойные.

 К однослойным относятся так называемая модель Хопфилда и последующие ее модификации, а также сеть, известная под названием «машина Больцмана».

 Многослойная сеть имеет входной, выходной и скрытые слои: на входной подается информация, с выходного снимается ответ, скрытые слои участвуют в обработке. Число нейронов во входном и выходном слоях определяется обучающей выборкой (примерами с известным решением) и задается на этапе постановки задачи. А размеры скрытой части, как правило, выбираются «методом проб и ошибок», который зачастую отнимает немало времени и не гарантирует хорошего результата.

 Изменяя структуру связей и весовые коэффициенты, можно обучать нейронную сеть решать определенные задачи. Основные задачи, с которыми хорошо справляются нейронные сети,— это задачи классификации или, говоря по-другому, распознавания образов.

 Тот нейрон, что используется при компьютерном моделировании нейронных сетей, только отдаленно похож на нейрон головного мозга. Элементы, используемые при моделировании нейронных сетей, принято называть формальными нейронами (Гутчин, и др., 1967).

 Как устроен формальный нейрон?

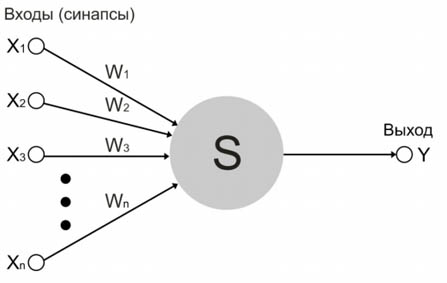
Рисунок 6. Математическая модель одиночного формального нейрона.

На входы нейрона Х (синапсы) подаются сигналы, которые могут быть внешними, а могут быть сигналами с выходов (аксонов) других нейронов. В нормальном состоянии нейрон неактивен, то есть на выходе Y — ноль (нет сигнала). Каждому входу сопоставлен весовой коэффициент W, определяющий «важность этого входа». Если сумма произведений сигналов на входе на весовые коэффициенты превышает некое пороговое значение — нейрон активируется (на выходе — единица) и продолжает быть активным, пока взвешенная сумма входов не опустится ниже порогового значения. В некоторых моделях формальных нейронов изменение выхода происходит скачкообразно, а в некоторых — в соответствии с сигмоидной логистической функцией.

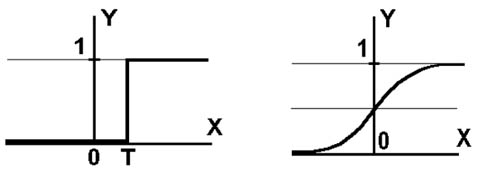
Рисунок 7. Скачкообразное и сигмоидное изменение состояния формального нейрона.

 Описанный формальный нейрон — это некая абстрактная конструкция, наделенная перечисленными свойствами, дающая возможность строить нейронные сети, применимые в определенных ситуациях. Еще раз подчеркнем, что такой формальный нейрон очень далек от реального нейрона головного мозга. Можно придумать другие формальные нейроны, обладающие более сложными свойствами,— например способные работать в разных режимах, каждому из которых свойственен свой алгоритм поведения. Более того, можно описать нейрон, одновременно работающий в нескольких режимах, и задать сложное информационное использование его связей. Такие более сложные формальные нейроны могут оказаться удобнее для решения специфических задач или служить иллюстрацией того, как работают реальные нейроны головного мозга.

 А теперь посмотрим, как может выглядеть нейронная сеть, решающая задачу распознавания цифр от 0 до 9.

 Предположим, что мы пишем цифры «от руки» на матрице 16х16 точек. Входом нашей нейронной сети будет информация о состоянии 256 точек, образующих нашу матрицу. Выходом нейронной сети будет информация о том, какая цифра от 0 до 9 распознана.

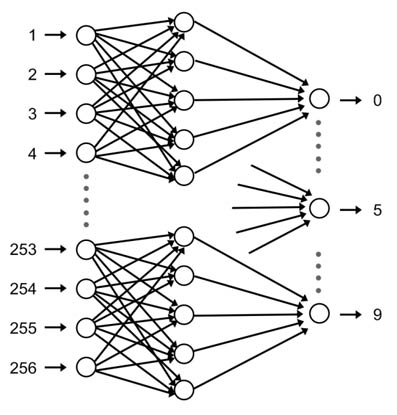
Рисунок 8. Нейронная сеть, распознающая цифры. Показана только часть нейронов и их связей.

 Запасемся обучающими примерами, то есть напишем одни и те же цифры разными способами (Рисунок 9).

Рисунок 9. Обучающие примеры.

Будем подавать множество таких примеров на вход нейронной сети и путем «шаманских» манипуляций менять веса у связей нейронов, добиваясь наилучшего соответствия сигналов на выходе с поданным тестовым примером.

 Существуют разные алгоритмы обучения нейронной сети. Выбор алгоритма зависит от топологии используемой сети, особенности задачи, времени, которое создатель нейронной сети готов потратить на ее обучение. Один из основных методов — это метод обратного распространения ошибки.

 Основная идея обратного распространения состоит в том, как получить оценку ошибки для нейронов скрытых слоев. Заметим, что известные ошибки, делаемые нейронами выходного слоя, возникают вследствие неизвестных пока ошибок нейронов скрытых слоев. Чем больше значение синаптической связи между нейроном скрытого слоя и выходным нейроном, тем сильнее ошибка первого влияет на ошибку второго. Следовательно, оценку ошибки элементов скрытых слоев можно получить как взвешенную сумму ошибок последующих слоев. При обучении информация распространяется от низших слоев иерархии к высшим, а оценки ошибок, делаемые сетью,— в обратном направлении, что и отражено в названии метода (Терехов, 1999).

 При оценке ошибки на каждом шаге можно записать зависимость ошибки и весовых коэффициентов конкретного нейрона. Минимизация ошибки — это нахождение минимума полученной функции, что делается дифференцированием полученной функции и поиском весовых коэффициентов, обращающих производную в ноль. Отсюда, кстати, становится понятным, почему в моделях, использующих этот метод, для описания работы нейрона применяется сигмоидная функция: в отличие от скачкообразной функции, она дифференцируема.

После обучения такая нейронная сеть начинает достаточно корректно распознавать не только тестовые примеры, но и другие, которых не было во время обучения.

 Обобщим.

Нейронные сети — это структуры, позволяющие перерабатывать информацию. То, как работает сеть, определяется конфигурацией связей, установленных между нейронами. В этой конфигурации содержится «память» об информации, полученной во время обучения. В обобщенном понимании нейронная сеть является самостоятельным объектом, не сводимым к другим, более простым, но обладающим теми же свойствами моделям.