Что такое паттерн?

Начнем с начала: что, собственно, такое паттерн? Слово это произошло от французского patron и обозначает просто некий шаблон, тему из повторяющихся событий или объектов. Если бы я попросил привести пример паттерна, вы, вероятно, назвали бы что-нибудь из визуальных элементов, присутствующих обычно в орнаментах и отделке; это могут быть полосы, зигзаги или узор горошком, рисунок на обоях в вашей спальне, расцветка любимых носков «ромбиками» или тонкая полоска на костюмной ткани. А может быть, вы подумали бы о паттернах в песенном ритме, о правильных чередующихся полосах слоев на скальном обнажении, об архитектурных элементах, о транспортных потоках и сигналах светофоров, об эмблемах автопроизводителей или фрагментах произведений искусства, к примеру, в работах Моне, Ван Гога и Рембрандта. Стандартные структуры (паттерны) из атомов водорода и кислорода образуют воду, паттерны замерзших кристалликов льда — снежинки, паттерны снегопада обеспечивают нам лыжню и т. д. Циклическую смену дня и ночи тоже можно назвать своего рода шаблоном, а тела наши следуют биологическим ритмам, связанным с 24-часовыми солнечными сутками. Мы редко вспоминаем о паттернах внутри себя, на самом же деле биологические закономерности в значительной мере определяют, кто мы и как себя чувствуем. У каждого из нас есть суточный цикл — биологические часы, которые 24 часа в сутки поддерживают регулярный стабильный ритм. После захода солнца мы испытываем усталость, на восходе — прилив энергии. Питается большинство людей тоже регулярно — завтрак, обед и ужин выстраиваются друг за другом по заведенному порядку. У каждого из нас есть постоянные привычки, определяемые сменой дня и ночи, сна и бодрствования; кроме того, тело, поддерживая биохимическую активность, в разные моменты суток вырабатывает разные гормоны.

И, разумеется, без паттернов невозможны компьютерные программы, язык, литература и математика, определяемая обычно как «наука о структурах, порядке и отношениях». Любая последовательность чисел, которую можно задать математической функцией, считается упорядоченной (то есть представляет собой своеобразный паттерн). Возможно, такие паттерны сложнее выявить, чем многие другие, но для тренировки ума они подходят замечательно. Рассмотрим несколько для разминки.

2, 4, 6, 8, 10, __, __, __. (Можете ли вы определить недостающие числа?)

Это очень простой пример: последовательность четных чисел. А вот еще один:

77, 49, 36, 18, __. (Можете ли вы определить следующее число?)

Вот как это действует:

Семью семь — произведение двух цифр первого числа, равное сорока девяти — это второе число в серии. Далее снова: четырежды девять равняется тридцати шести; это третье число. И далее по тому же принципу: трижды шесть будет восемнадцать; это четвертое число. Единожды восемь — восемь; это пятое недостающее число серии. Здорово, правда?

Иногда закономерности приходится искать другими, более тонкими способами. Я покажу вам несколько примеров на вычисление произведения двух чисел. Попробуйте найти закономерность в способе расчета. Может быть, сразу вы ее не увидите, поэтому не спешите. Это упражнение само по себе отлично помогает разбудить мозг.

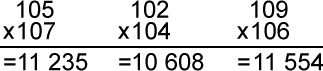
Подсказка: Этот способ работает только при перемножении двух чисел от 100 до 109. Все ответы должны быть пятизначными числами.

Внимание: во многих упражнениях я при объяснении решения буду использовать такие понятия, как «цифра разряда десятков» и «цифра разряда единиц». Это помогает мне точно называть числа. Если вы нуждаетесь в пояснении, то вот оно:

В числе 123 «3» — цифра единичного разряда (число единиц), «2» — цифра разряда десятков (число десятков), и «1» — цифра разряда сотен (число сотен).

Ответ: Первая цифра результата — всегда единица. Следующие две цифры результата, или «среднее» число, находится путем сложения цифр единичного разряда в каждой задаче. Так, при перемножении 105 и 107, вы складываете 5 и 7 и получаете 12; при перемножении 102 и 104 складываете 2 и 4 и получаете 6. Но имейте в виду: в «среднем» числе должно быть две цифры, так что перед 6 придется поставить 0. При перемножении 109 и 106 вы складываете 9 и 6 и получаете 15. Наконец, чтобы получить последние две цифры результата, нужно перемножить цифры единичного разряда в каждом примере. Так, для чисел 105 и 107 вы умножаете 5 на 7 и получаете 35; для чисел 102 и 104 умножаете 2 на 4 и получаете 8. Опять же, на этом месте не может стоять одна цифра, поэтому перед восьмеркой ставим 0. Наконец, при перемножении 109 и 106 вы умножаете 9 на 6 и получаете 54.

Можете рассмотреть еще несколько аналогичных примеров. Цель этого упражнения — не столько научить вас упрощенному способу перемножения чисел от 100 до 109, сколько помочь вам заставить свой мозг обращать внимание на закономерности и проделывать всякие фокусы. (Не забывайте, все решения можно найти в конце главы.)

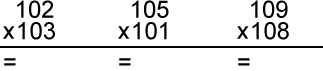
Хорошо, немного усложним задачу. Ниже вы найдете способ возведения в квадрат чисел шестого десятка. Отыщете закономерность?

56² = 3136

53² = 2809

58² = 3364

54² = __?

Подсказка: Уберите 5 и поищите закономерность.

Ответ: 2916.

Решение: В каждом случае квадрат цифр единичного разряда (6², 3², 8²) исходного числа дает две последние цифры ответа (36, 09 и 64 соответственно). Именно поэтому я посоветовал вам для начала убрать пятерку, чтобы легче было это заметить. Теперь нужно возвести в квадрат 5 (5²), что даст нам 25. Затем добавьте к 25 цифру единичного разряда. Так, в случае 56² у нас 25 + 6 = 31; в случае 53² прибавим 3 к 25, и получим 28; в случае 58² складываем 25 и 8, получаем 33. Давайте вычислим 54² вместе:

• Возводим в квадрат цифру единичного разряда, 4 x 4 = 16. Это две последние цифры ответа.

• Берем 5 раз по 5, получаем 25 и прибавляем цифру единичного разряда, 25 + 4 = 29. Это дает нам первые две цифры ответа.

• Ответ: 2916.

Все понятно? Если нет, вернитесь и еще раз все продумайте. Потренируйтесь. Добейтесь, чтобы это упражнение вы могли выполнять в уме быстро и легко. Вот еще примеры:

57² = __.

55² = __.

59² = __.

51² = __.

52² = __.

Паттерны — это не обязательно сложный ряд различных цифр или других объектов. Они могут быть «проще» и представлять собой, к примеру, сложную последовательность одинаковых цифр или предметов. Первое, что приходит на ум в качестве примера, — это двоичный код. Слово «двоичный» относится к тому, что состоит из двух частей. Нам часто приходится слышать, что двоичный код — это способ представления текста или процессорных команд при помощи двух цифр двоичной системы счисления, 0 и 1. Для этого каждому символу или каждой команде ставится в соответствие так называемая бинарная (двоичная) последовательность. К примеру, двоичная последовательность из восьми цифр (бит) может представлять любое из 256 возможных значений, а потому может соответствовать множеству различных символов, букв или команд. Даже если вы не понимаете, что все это на самом деле означает, достаточно сказать, что возможностью создавать компьютеры и сложные программы для них мы в значительной мере обязаны простым комбинациям нулей и единиц.