Декартовы координаты
Примечание. На диаграмме, представленной на рис. 5.1, знак ~ символизирует «не». Поэтому эту иллюстрацию следует читать так: суждение = A, B, инверсия = A, не B, конверсия = не A, B, незеркальный реверс образа = не A, не B. Мне (Б. Б.) нравится думать об этом в терминах (—) и (+). При помощи данного способа это читалось бы так: суждение = (+) (+), инверсия = (+) (—), конверсия = (—) (+) и незеркальный реверс образа = (—) (—).

Рис. 5.1. Декартовы координаты
Оувердарф и Сильверторн (Overdurf & Silverthorn, 1996) в книге «По ту сторону слов» привели несколько прекрасных метафор, помогающих объяснить картезианскую логику. Они используют аналогию с перчаткой и говорят, что инверсией перчатки была бы вывернутая наизнанку перчатка. Конверсией перчатки была бы другая перчатка, то есть перчатка для другой руки.
Незеркальный реверс образа перчатки включал бы все, существующее в мире, кроме перчатки. Другим способом рассмотрения незеркального реверса образа в контексте суждения о проблеме является утверждение, что незеркальный реверс образа включает все, из чего проблема не состоит. В чем сила данного подхода? Как только мы вводим незеркальный реверс образа проблемы, проблема исчезает. Это вызвано тем, что «все остальное» незеркального реверса образа поглощает проблему. Исчезает то, что определяло проблему.
Джулия Сильверторн приводит другой пример визуальной метафоры. Эта метафора касается приготовления желе. Предположим, что форма для желе поставлена в тарелку или миску большей глубины и большего диаметра. Если вы зальете желе в форму, вы получите желе, имеющее соответствующую форму. Но если при заливании желе в форму вы обнаружите, что она протекает, то сначала все желе попадет в форму, а затем вытечет в большую миску. В конечном счете, и форма, и миска будут заполнены и желе в большей миске «поглотит» желе в форме. Фактически, форма для желе исчезнет и, в конечном счете, ее наличие не будет играть никакой роли.
В случае паттерна незеркального реверса образа «все остальное» поглощает суждение, и, если суждение не играет для человека никакой роли, оно исчезнет как проблема.
Помимо приведенных выше хорошо сформулировать желаемый результат помогают также следующие вопросы:
Могу ли я проверить результат?
Могу ли я разукрупнить результат на достижимые части?
Нам следует уделить особое внимание тому, чтобы не делать наши результаты слишком глобальными. В случае хорошо сформулированного результата мы должны разбить результат на последовательность операций. Это позволит нам понять и систематизировать способ достижения результата.
Знаю ли я, какой первый шаг я должен предпринять?
Чувствую ли я, что первый шаг будет успешным?
Если я достигну результата, будет ли он соответствовать моим ценностям?
Могу ли я найти больше одного способа достижения результата?
Какие подходящие личные якоря существуют в том контексте, в котором я желаю получить результат?
Обладаю ли я достаточной информацией о внутреннем состоянии, необходимом для достижения результата?
Есть ли у меня устойчивый образ результата?
Имею ли я в своем сознании звуки, картины, слова и ощущения, связанные с желаемым результатом?
Направляет ли мое внутреннее состояние мое поведение к достижению результата?
Питер Янг дает следующий визуальный образ хорошо сформулированного результата (рис. 5.2).
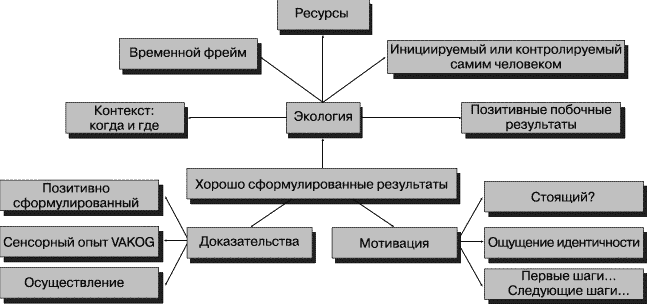
Рис. 5.2. Хорошо сформулированные результаты
Более 800 000 книг и аудиокниг! 📚
Получи 2 месяца Литрес Подписки в подарок и наслаждайся неограниченным чтением
ПОЛУЧИТЬ ПОДАРОК