4.3 Геометрические модели как современный образ науки

Мудрые высказывания авторитетных ученых всех эпох о роли геометрии и числа в познании мира могли бы составить объемную книгу, поскольку «закономерности геометрии являются самыми общими и простирают свою власть и значимость на любые события и явления в мире, который мы знаем» (Чернин, 1987, c. 30).

«В наши дни – после Эйнштейна – время геометризировалось. Появилась тенденция говорить не о пространстве и времени в отдельности, а о геометрии в ее абстрактном проявлении. Геометрия оказывается тем исходным априорным синтетическим знанием, которое делает возможным созерцание как внешнего, так и внутреннего мира. Различные геометрии раскрывают различные ракурсы видения мира. Образы геометрий, несмотря на всю их абстрактность, легко созерцаемы. Обращение к мере как к проявлению числа – это на самом деле путь к геометризации» (Пригожин, 1989, с. 16).

Именно пространственно организованные (геометрические) модели и имманентно присутствующие в них соотношения структурных компонентов могут быть той универсальной базовой моделью-образом, с помощью которой мы можем адекватно анализировать большую часть явлений окружающего мира. Как уже отмечалось, обращение к «особой действительности объекта», своего рода пространственному образу психического, впервые осуществлено в работе В.П. Зинченко и М.К. Мамардашвили, опубликованной ими в 1977 году.

Модели, которые в состоянии достоверно описать психические системы, определяются как базовые динамические модели. Как отмечают Д.С. и Н.М. Чернавские (2003), подобные модели должны содержать гипотетический элемент, который, по существу, аксиоматизируется.

Возникают закономерные вопросы:

1. Какой вид базовой динамической модели наиболее адекватен и эффективен при анализе образа психического в целом и его компонентов?

2. Можно ли ограниченным числом однотипных моделей описать всю совокупность психологических явлений и других проявлений органических и неорганических форм существования? Какими особенностями и свойствами должна обладать подобная модель «универсума»?

а

б

в

г

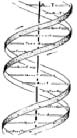
д

е

Рис. 4.1. Структурное (фрактальное) единство мироздания а) Одна из современных моделей Вселенной (Стахов, Слученкова, Щербаков, 2007); б) Спиралевидность галактики; в) Спираль моллюска рода Nautilus; г) Филлотаксическая структура сосновой шишки; д) Модель спирали ДНК; е) Модель периодизации развития по Д.И. Фельдштейну (1999); ж) Геометрическая модель психического развития (Семаго М.М., 2007а)

Ответ на первый вопрос дает использование геометрических модельных представлений.

Ответ на второй был дан в главе 3 введением принципа, определяющего базовый и универсальный характер динамической модели, – принципа фрактальности (изоморфности, самоподобия) всех структур существующего мироздания (Семаго М.М., 2008, 2009в).

Как уже отмечалось, изоморфные структуры можно обнаружить практически во всех компонентах мироздания. Подобные объекты имеют пространственную протяженность и конфигурацию, которая и сама обладает свойством фрактальности. Остается определить геометрическую форму, которая должна быть положена в основу базовой модели. И здесь имеет смысл обратиться к уже имеющимся геометрическим универсалиям, которые пронизывают всю историю человечества и культуру, встречаются в неорганической и органической природе. В данном случае мы говорим об образе спирали.

Спиральность развития составляет одну из наиболее фундаментальных и закономерных форм: от галактик до полипептидных цепей нуклеотидов, раковины моллюска наутилуса и сосновой шишки (рис. 4.1), от спиралевидного строения стеблей растений (явление филлотаксиса) до траектории подъема птиц с водной поверхности (этология). «Везде обнаруживается логарифмическая спираль как инвариант структурного развития, атрибут уровневого строения систем материального мира» (Сороко, 2006, с. 86). Такое широкое распространение в живой природе спиралевидных форм еще И.В. Гете считал математическим символом жизни и духовного развития, что подтвердило открытие молекулы ДНК, имеющей структурную форму вложенных друг в друга спиралей.

Речь идет о высокой общности (практически для всех эволюционных уровней) существования природных объектов в виде спирали, в частности, в виде конусных логарифмических спиралей. Спиралевидная конусная структура – одно из проявлений закона структурной гармонии систем и обобщенных фибоначчиевых инвариант.

Как и многие другие мировоззренческие универсалии, образ спирали впервые появляется в мифологиях народов мира. Это один из образов, символизирующих эволюцию мира. Спираль – это одновременно и этапы (последовательность) эволюции, и ее цикличность. В данном случае, наряду с универсальной формой этот образ реализует и еще одну мирозданческую универсалию – золотую пропорцию как отражение структурной гармонии.

Для нас важно, что этот образ-модель отвечает всем необходимым характеристикам динамических базовых моделей и, следовательно, может быть адекватно применен и к моделированию психических процессов, систем и к психическому развитию в целом.

Интересно, что в современных космогонических представлениях об эволюции Вселенной присутствуют специфические конусообразные структуры, спиралевидные мегагалактические образования обнаружены во Вселенной. Таким образом, и конус, и спираль, развертывающаяся по его поверхности, являются фрактальными атрибутами мироздания, его образной универсалией.

Приведем наиболее показательные примеры анатомического и функционального обеспечения психического развития, которые построены на тех же базовых универсалиях.

Одним из таких примеров является анатомия всем известного органа слухового восприятия. Напомним, что костная улитка – спирально извивающийся канал, образующий два с половиной оборота вокруг стержня конической формы. По форме она очень напоминает виноградную улитку, откуда и получила свое название. Другой пример – это пространственная конфигурация головного мозга, которую, в известном приближении, можно аппроксимировать не какой-либо, а именно конусной фигурой, что свидетельствует о фрактальной атрибутивности и этого природного объекта. Все вышесказанное позволяет предположить, что в анализе психического, его структурных компонентов использование конусно-спиралевидных моделей-образов окажется достаточно эвристичным и прогностично оправданным.

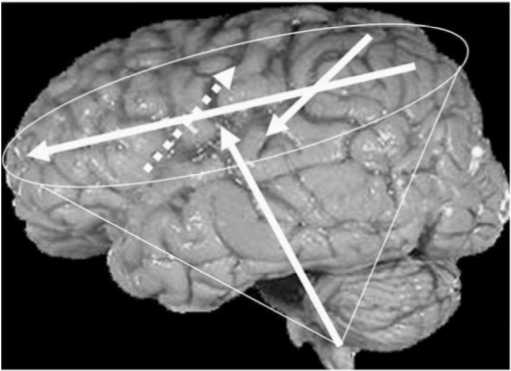
Рис. 4.2. Упрощенная реконструкция векторного «перераспределения» организации психических функциональных систем в «пространстве» головного мозга

В качестве одного из примеров анализа функционального обеспечения психических процессов можно привести объемно организованную модель процесса кортикализации психических функций в онтогенезе (Семенович, 2001). В соответствии с этой моделью в процессе развития действуют три вектора (направления) перераспределения (в том числе и кортикализации) кортикализации психических функций: «снизу вверх», «справа налево» и «сзади вперед»[35](рис. 4.2).

Причем в норме кортикализация психических функций (в том числе процесс прогрессирующей латерализации) по всем трем направлениям происходит в онтогенезе фактически симультанно. Если мысленно представить результат подобного «движения», то мы также получим конусовидно организованную спиральную траекторию простроения функциональной организации. В этом факте проявляется интересная геометрическая аналогия анатомической конфигурации головного мозга и процесса кортикализации психических функций, подтверждающая в определенном смысле возможность использования единой модели-образа, и для природных явлений, и для анализа психического.

Анализ психического развития, его отдельных аспектов с точки зрения предлагаемой «геометрической» методологии достаточно объемен и выходит за пределы данной монографии. Мы приводим лишь пример эффективности использования подобного анализа (распространение конусно-спиральной модели на периодизацию психического развития) в Приложении 2. В наших работах представлены и другие варианты использования конусных и спиральных моделей в диагностической и коррекционно-развивающей деятельности психолога (Семаго, 2008, 2009в). В целом мы считаем эффективным и эвристичным использование подобных геометрических образов как аналогов различных аспектов психического развития. Естественно, подобные модели нуждаются в дальнейшей более детальной разработке.