Думатель и анализатор

Думатель и анализатор

Ах, как было хорошо быть уверенным, что находящийся у нас в голове думатель и анализатор — АС, всегда остановит нас, когда мы готовы принять необдуманные решения или совершить опрометчивые поступки! Увы, об этом можно только мечтать. Наша аналитическая система — «существо» очень ленивое, даже предельно ленивое, а мы с вами являемся жертвами этой лености.

Как мы с вами уже знаем, одной из важнейших функций АС является мониторинг мыслей и действий, которые предлагает АКС и «допуск» их «к производству» или запрещение оных. Посмотрим, как это происходит в действительности. Для этого мы обратимся к знаменитому примеру Канемана, несколько его «русифицируя». Вам предлагается простейшая задача. Не пытайтесь решить её, а отвечайте сразу, полагаясь на вашу интуицию:

Ананас и яблоко стоят вместе 1 руб.10 коп. (цены условные).

Ананас на рубль дороже яблока.

Сколько стоит яблоко?

Совершенно естественно в вашем мозгу всплывает число и это число — 10 копеек. Задача решается слёту, ответ нетруден, круглая цифра привлекательна, но ответ абсолютно неправилен!

Теперь немного напрягитесь, вспомните арифметику и вам станет ясно, что правильный ответ — 5 копеек. Те из вас, кто сразу получил правильный ответ, может поздравить себя — их аналитическая система иногда пытается противостоять лёгким интуитивным решениям, подсказываемым АКС.

Шэйн Фредерик и Дэниэл Канеман предлагали решать эту задачу студентам различных американских университетов. Более 50 % обучающихся в Гарварде, Принстоне и Массачусетском технологическом институте дали неправильный ответ, среди студентов не столь престижных университетов процент доходил до 80! Аналитическая система этих людей явно доверяла интуитивным решениям АКС и не была готова предпринять даже малейшие усилия для проверки результата, активно избегала неприятного напряжения. Эти люди верили в силу своей интуиции и что особенно интересно, никому в голову не пришёл вопрос, почему им предлагают решить столь простую задачу!

Ещё один пример Канемана. Простой логический силлогизм. Попытайтесь быстро определить, правилен ли вывод.

Все розы являются цветами.

Некоторые цветы быстро вянут.

Следовательно, некоторые розы вянут быстро.

Большинство студентов посчитали этот вывод правильным, что однако не так, ибо возможно, что розы не входят в число быстровянущих цветов.

Как и в предыдущем примере, правдоподобный ответ появляется в сознании мгновенно и «передумать» его крайне сложно, ведь вас всё время преследует идея, что ответ всё-таки правильный. Большинство людей и не затрудняются это делать.

Обратимся теперь к задаче, разработанной Питером Вэйсоном (Wason, P. C. 1968)[6].

Представьте, что перед вами лежат четыре карточки. Каждая из них имеет с одной стороны букву, а с другой — цифру. Существует правило: если на карточке нарисована гласная, то с другой стороны будет обязательно чётное число. Как вы видите, на двух карточках нарисованы буквы, а на двух других — цифры. Ваша задача: решить, какую карточку или какие карточки следует перевернуть, чтобы определить, является ли вышеуказанное правило верным. Запишите полученный результат.

Эта так называемая «задача выбора из четырёх карт» была очень интенсивно исследована психологами. Прежде всего по двум причинам: большинство людей понимают задание неправильно и крайне тяжело понять почему. Ответ кажется очевидным. Гипотетическое правило — если карточка имеет гласную на одной стороне, то на другой стороне обязательно будет чётное число. Таким образом кажется, что следует перевернуть карточки «А» и «8», поскольку «А» является гласной и следует проверить, изображено ли чётное число на обратной стороне, а «8» (чётное число) — чтобы посмотреть, есть ли на обратной стороне гласная.

Проблема состоит в том, что этот ответ, который дают более 50 % исследуемых, является ложным!

Второй наиболее распространённый ответ — перевернуть только карточку «А» (чтобы проверить, изображено ли чётное число на обратной стороне). Этот ответ был получен у более чем 20 % опрошенных и он тоже неверен!

Ещё 20 % переворачивали другие комбинации карточек (например, «8» и «К»), что также некорректно.

Если вы принадлежите к 90 % людей, опрошенных в десятках исследований в последние 40 лет, то вы тоже дали неверный ответ.

Теперь посмотрим, почему люди ошибаются при ответе на эту задачу. Первое, они правы, когда речь идёт о «К» и «А» карточках. Большинство людей выбирают «А» и не выбирают «К». Поскольку в правиле нечего не сказано о том, что должно быть изображено на обратной стороне карточек с согласными буквами, они совершенно не релевантны для проверки правила. Что неверно для «А». Эта карточка может иметь на обратной стороне чётное или нечётное число. И хотя первое подтверждает правило, второе может доказать его ложность. Короче говоря, для того, чтобы доказать, что правило не ложно, необходимо перевернуть карточку с надписью «А». На этом этапе большинство людей делают правильный выбор.

Проблемы возникают с карточками «5» и «8». Большинство людей делают здесь неправильный выбор. Они ошибочно думают, что должна быть выбрана карточка «8». Они предполагают проверить гипотезу, не находится ли на обратной стороне этой карточки согласная. Но, например, если бы на обратной стороне карточки «8» находилась «К», это бы не доказывало, что правило ложно, поскольку, хотя правило и говорит, что на обратной стороне карточки с гласной буквой должно находиться чётное число, в правиле не написано, что на обратной стороне карточки с чётным числом должна находиться гласная буква! Таким образом, если на обратной стороне карточки с чётным числом находится согласная, это ничего не говорит о ложности или правильности.

Напротив, карточка, на которой изображено число «5», очень существенна для проверки правила. Эта карточка может иметь с обратной стороны гласную и тогда правило ложно. То есть, для того, чтобы проверить правило, карточку «5» выбрать абсолютно необходимо. Таким образом, правильный ответ гласит — необходимо выбрать карточки «А» и «5».

Резюмируя, мы можем сказать, что наше правило сформулировано в виде условия: «если P то Q». Ложным в данном случае является «если P то не-Q». Почему же для большинства людей так сложно решить эту задачу? Первое, что приходит в голову — задание слишком абстрактно, если бы речь шла о событиях реального мира, то результат был бы совершенно другим. Так ли это? Для проверки этого предположения была предложена «Проблема пункта назначения».

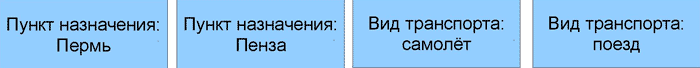
На каждой карточке напечатан с одной стороны пункт назначения, а с другой — вид транспорта. Правило гласит: если с одной стороны напечатано «Пенза», то с другой стороны должно стоять «самолёт». Ваша задача — выяснить, какие карточки следует перевернуть, чтобы проверить, является ли правило верным или ложным.

Удивительно, но «реальное» содержание задачи абсолютно не влияет на результат. Большинство людей всё равно переворачивали либо «Р»(Пенза) и «Q»(самолёт), либо «Р» только. Правильный же ответ «Р»(Пенза) и «не-Q»(поезд), дался только незначительному количеству опрошенных.

Почему же эта задача так сложна? Множество теорий пытались это объяснить. В частности, людям (включая учёных) очень сложно думать о том, что не подтверждает, а опровергает их гипотезы. Согласно данной теории это то, что заставляет людей переворачивать карточку «Р» (в попытке подтвердить «Q») и карточку «Q» (в попытке подтвердить «Р»), абсолютно не обращая внимания на карточку «не-Q»(которая может привести к неподтверждению «Р»).

Наиболее распространённым однако является объяснение, предложенное психологом Джонатаном Эвенсом (Jonathan Evans, Matching bias and set sizes: A discussion of Yama, 2002)[7], попадающее в наиболее популярный в последние два десятилетия тренд когнитивной психологии — эвристики и ошибки.