Два с половиной измерения

Что же эксперты, закончив работу, помещают на доску объявлений, к которой есть доступ у всего остального мозга? Если бы мы могли каким-то образом показать зону видимости с точки зрения остального мозга – как будто с точки зрения гипотетической камеры, скрывающейся внутри глаза Терминатора, – какой бы она была? Может показаться, что этот вопрос тоже основан на ошибочном выводе о существовании «глупого человечка в голове», но это не так. Речь идет об информации, которая содержится в одной из репрезентаций данных в мозге, и о том, какую форму принимает информация. Более того, если воспринимать этот вопрос серьезно, то это может стать настоящим ударом по нашим наивным представлениям о мысленном взоре.

Эксперты по стереоизображению, движению, контуру и затенению серьезно потрудились, чтобы у нас было третье измерение. Было бы вполне естественно воспользоваться плодами их трудов, чтобы построить трехмерную репрезентацию мира. Мозаика на сетчатке, в виде которой отображается воспринимаемая картинка, уступает место ментальной песочнице, в которой ей придают объем; изображение становится масштабной моделью[267]. Трехмерная модель соответствует нашему принципиальному пониманию мира. Когда ребенок на наших глазах становится то больше, то меньше размером, мы знаем, что мы не в Стране чудес, где можно от одной таблетки вырасти, а от другой уменьшиться. И в отличие от пресловутого страуса (история про которого, кстати, вымышлена) мы не считаем, что объекты исчезают, стоит нам отвернуться от них или закрыть их. Мы справляемся с реальностью только потому, что в своих мыслях и действиях руководствуемся знаниями об этом огромном и устойчивом материальном мире. Вероятно, зрение дает нам это знание в форме масштабной модели.

В самой теории масштабной модели нет ничего подозрительного. Многие программы автоматизированного проектирования используют программные модели реальных объектов, а аппараты компьютерной и магнитно-резонансной томографии строят их с помощью сложных алгоритмов. Трехмерная модель использует список из миллионов координат крошечных кубиков, которые образуют твердое тело; их называют элементами объема, или вокселями (от англ, volume: «объем»), по аналогии с элементами изображения, или пикселями (от англ, picture: «изображение»). Каждая тройка координат соотнесена с элементом информации – таким, как плотность ткани в данной точке тела. Конечно, если бы мозг хранил информацию в форме вокселей, они не были бы расположены в голове в виде трехмерного кубика – и внутри компьютера они точно так же не образуют трехмерный кубик. Важно лишь то, что к каждому вокселю привязана совокупность нейронов, и паттерны возбуждения этих нейронов могут отражать содержание вокселя.

Вот тут нужно еще раз подчеркнуть, что в этой схеме не может быть никакого гомункула. Нет ничего плохого в идее о том, что некий программный демон, или алгоритм поиска, или нейронная сеть получает доступ к информации по масштабной модели, но только если не забывать о том, что этот доступ к информации осуществляется напрямую: в форме координат вокселей, поступающих на ввод и на вывод. Не нужно думать, что алгоритм поиска видит масштабную модель. Вокруг этого «наблюдателя» непроглядная тьма, а у него самого нет ни хрусталика, ни сетчатой оболочки, ни даже точки наблюдения; он нигде и везде. Нет ни проекции, ни перспективы, ни видимой зоны, ни затенения. Более того, сама масштабная модель и нужна для того, чтобы избежать всех этих неудобств. Если вы хотите говорить о гомункуле, представьте себе, что вы исследуете масштабную модель города размером с комнату в темноте. Можно блуждать по этому городу, подходить к каждому зданию с разных сторон, ощупывать его стены, засовывать пальцы в окна и двери, чтобы узнать, что у него внутри. Если схватитесь за здание рукой, его стены всегда будут параллельны друг другу, независимо от того, держите ли вы его близко к лицу или на расстоянии вытянутой руки. Или представьте, что вы трогаете руками маленькую игрушку или конфету во рту. Но зрение – даже трехмерное, свободное от иллюзий зрение, ради которого мозг затрачивает такие колоссальные усилия – не имеет с этим ничего общего! В лучшем случае у нас есть абстрактное представление о стабильной структуре мира вокруг нас; ослепительное великолепие цвета и формы, моментально захлестывающее наше восприятие, как только мы открываем глаза, – нечто совершенно иное.

Во-первых, зрение – это не театр, где мы видим сцену полностью. Мы живо ощущаем только то, что у нас перед глазами; мир за периметром поля зрения и позади нас известен нам лишь очень приблизительно, можно сказать, на мыслительном уровне. (Я знаю, что позади меня есть полка, а передо мной – окно, но я вижу только окно, а полку не вижу.) Более того, глаза несколько раз за одну секунду мелькают с места на место, и та часть поля зрения, что не попадает в «прицел» центральной ямки (фовеа), предстает перед нами на удивление размытой. (Попробуйте держать руку сантиметрах в десяти от линии взора; вы обнаружите, что вам сложно сосчитать собственные пальцы.) Я не просто анализирую анатомическое устройство глазного яблока. Можно подумать, что мозг собирает что-то вроде коллажа из снимков, сделанных во время каждого взгляда – как панорамный фотоаппарат, который экспонирует один кадр, поворачивается по вертикальной оси на точное расстояние, экспонирует следующий отрезок пленки и так далее, пока не получится бесшовное панорамное изображение. Однако мозг – не панорамный фотоаппарат. Лабораторные исследования показали, что когда человек совершает движение глазами или головой, он немедленно теряет информацию о графических деталях того, на что он смотрел[268].

Во-вторых, наше зрение – не рентген. Мы видим поверхности, а не объем. Если вы видели, как я кладу предмет в коробку или прячу за деревом, то вы знаете, что он там, но не видите его и не можете рассказать в подробностях о том, как он выглядит. Опять же это говорит о том, что мы – не супермены. Мы, простые смертные, могли бы иметь фотографическую память, которая модифицирует трехмерную модель, дополняя нужные места информацией, полученной из увиденного ранее. Но у нас ее нет. Если говорить о подробностях изображения, здесь будет вполне справедлива поговорка «с глаз долой – из сердца вон».

В-третьих, мы видим в перспективе. Когда мы стоим между железнодорожными рельсами, нам кажется, что на горизонте они сходятся. Конечно, мы знаем, что на самом деле они не сходятся; если бы это было так, поезд сошел бы с рельс. Но мы не можем не видеть их как сходящиеся линии, даже несмотря на то, что наше ощущение глубины дает мозгу массу информации, которую мозг мог бы потенциально использовать, чтобы компенсировать этот эффект. Точно так же мы видим, что движущиеся объекты увеличиваются, уменьшаются, укорачиваются. С настоящей масштабной моделью такого произойти не может. Естественно, зрительная система в определенной степени устраняет эффект перспективы. Люди, которые не занимаются живописью, не замечают, что ближний угол стола проецируется как острый угол, а дальний – как тупой угол; им кажется, что и тот, и другой выглядят как прямые углы, какими они и являются в реальности. Однако железнодорожные рельсы – доказательство того, что полностью устранить эффект перспективы нельзя.

В-четвертых, в строгом геометрическом смысле слова мы видим не в трех, а в двух измерениях. Математик Анри Пуанкаре обнаружил простой способ определить количество измерений той или иной вещи. Нужно найти объект, который разделяет вещь на две части, сосчитать количество измерений этого разделителя и прибавить единицу. Точку нельзя разделить вовсе; следовательно, у нее ноль измерений. У линии – одно измерение, потому что ее можно разделить на две части точкой. У плоскости – два измерения, потому что ее может разрезать надвое линия, но не точка. У сферы – три, потому что ее может расколоть пополам только двухмерное лезвие; дробинкой или иголкой ее не расколоть. А как же поле зрения? Его можно разделить линией. Например, горизонт делит поле зрения пополам. Когда мы стоим перед туго натянутым проводом, все, что мы видим, оказывается по одну или по другую сторону от него. Периметр круглого стола тоже делит поле зрения на две части: любая точка поля зрения оказывается либо внутри, либо снаружи периметра. Добавим единицу к одномерности линии и получим два. Если опираться на этот критерий, поле зрения двухмерно[269]. Кстати говоря, это не означает, что зрительное поле – это плоскость. Двумерные поверхности могут быть изогнуты и образовывать третье измерение – как резиновая формочка или блистерная упаковка.

В-пятых, мы видим не непосредственно «объекты», передвигаемые куски вещества, которые мы можем считать, классифицировать и называть именами. В том, что касается зрения, мы даже не можем точно сказать, что такое объект. Дэвид Марр, рассуждая о том, как построить компьютерную зрительную систему, был вынужден задаться вопросом:

Можно ли сказать, что нос – объект? А голова? А является ли голова объектом, если она присоединена к телу? А как насчет человека на лошади? Эти вопросы показывают, что сложности, связанные с попытками сформулировать, какую часть изображения следует распознать как одну область, так значительны, что они практически равносильны философским проблемам. На них вообще нет ответа – любая из перечисленных вещей может быть объектом, если вам угодно рассматривать ее с этой точки зрения, или частью более крупного объекта.

С помощью капельки суперклея можно сделать из двух объектов один, но наша зрительная система не может знать этого.

Тем не менее у нас есть почти осязаемое чувство поверхностей и границ между ними. Самые знаменитые оптические иллюзии в психологии – результат постоянного стремления мозга разделить видимое пространство на поверхности и решить, какая из них расположена перед какой. Один из таких примеров – ваза-лицо Рубина, в которой можно увидеть кубок и два лица, смотрящих друг на друга. Одновременно и лица и вазу увидеть нельзя (даже если представить, что два человека держат кубок, зажав его между носами), и какая бы фигура не оказалась в данный момент доминирующей, она «забирает себе» границу в качестве демаркационной линии, оставляя второй части рисунка роль аморфного фона.

Еще один пример – треугольник Каниссы, пустота, частично перекрывающая фигуру, которая кажется столь же реальной, как если бы она была изображена чернилами.

Лица, ваза и треугольник – знакомые нам объекты, однако успешность иллюзии не связана с тем, что они нам знакомы; не менее интересными были бы в этой роли и бессмысленные пятна.

Мы воспринимаем поверхности неосознанно, под воздействием информации, поступающей от сетчатки глаза; вопреки распространенному мнению мы не видим то, что хотим увидеть[270].

Что же представляет собой продукт видения? Марр называет его «2,5-мерный эскиз»[271]; другие ученые используют термин «представление видимой поверхности»[272]. Глубине отводится необычная роль половины измерения, поскольку она не является определяющей для способа передачи визуальной информации (в отличие от вертикального и горизонтального измерений); это всего лишь один из элементов информации, сообщаемой этим носителем. Представьте игрушку, состоящую из сотен подвижных штырьков, которую можно прижать к трехмерной поверхности (например, к лицу), и на обратной стороне получится очертание этой поверхности. Очертание имеет три измерения, но они не равноценны. Положение по вертикали и положение по горизонтали определяются тем, какие из штырьков оказались затронуты, а положение по глубине определяется тем, как далеко выдвинулся тот или иной штырек. Для любой глубины может быть задействовано множество штырьков; для любого штырька может быть только одна глубина.

2,5-мерный эскиз выглядит как что-то вроде этого:

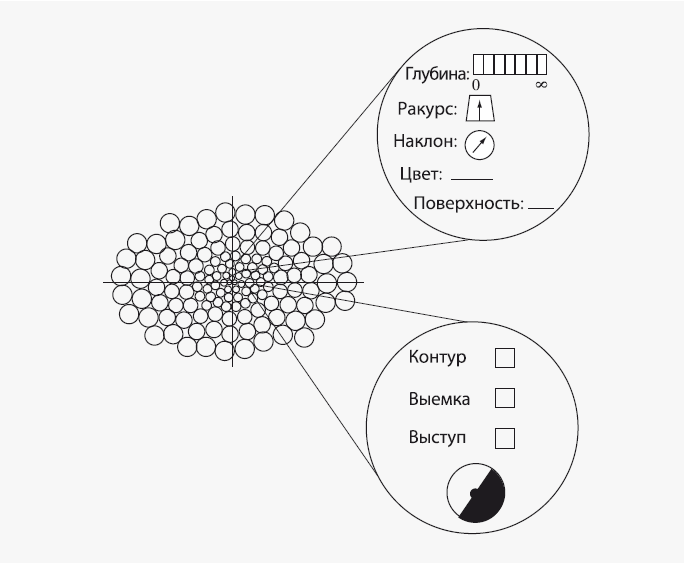
Это мозаика из ячеек, или пикселей, каждый из которых соответствует линии взора с точки зрения циклопического глаза. Ширина мозаики больше высоты потому, что наши глаза располагаются в черепе рядом, а не друг над другом. Ячейки в центре поля зрения меньше, чем на периферии, потому что разрешение в центре выше. Каждая ячейка может представлять информацию о поверхности или ее кромке, как если бы у нее были две отдельные формы с пробелами, которые можно заполнить. Форма для участка поверхности включает в себя графы для глубины, ракурса (параметра, определяющего, насколько поверхность наклонена назад или вперед), наклона (насколько она накренена влево или вправо) и цвета, а также ярлык, соответствующий тому, частью какой поверхности она является. Форма для участка границы включает в себя графы, в которых можно отметить, является ли он элементом контура объекта, выемки или выступа; кроме того, имеется круговая шкала для определения ориентации, которая показывает (в случае, если речь идет о контуре объекта), какая сторона относится к поверхности, которая «обладает» границей, а какая – всего лишь фон. Конечно, в буквальном смысле у нас в голове нет никаких канцелярских форм. Приведенная схема – это макет, отображающий виды информации в 2,5-мерном эскизе. Мозг, по-видимому, использует пучки нейронов и их возбуждение, чтобы хранить и передавать информацию от одной корковой зоны к другой – наподобие карт в судовом журнале.

Почему же мы видим в двух с половиной измерениях? Почему не строим модель в голове? Ответ на этот вопрос отчасти связан с издержками и выгодами хранения информации. Любой пользователь компьютера знает, что графические файлы – просто ненасытные пожиратели дискового пространства. Вместо того чтобы собирать гигабайты входной информации в сложную модель, которая незамедлительно станет устаревшей, как только хоть что-то сдвинется с места, мозг позволяет самому миру хранить информацию, которая выходит за пределы взгляда. Стоит нам немного повернуть голову или переместить взгляд – и загрузится новый, уже измененный эскиз. Что же до второстепенного положения третьего измерения, это практически неизбежно. В отличие от двух остальных измерений, которые проявляются возбуждением в каждый конкретный момент того или иного количества палочек и колбочек, глубину мучительно сложно выжать из входных данных. Эксперты по стереоизображению, очертаниям, затенению и движению, отвечающие за вычисление глубины, имеют возможность передавать информацию о расстоянии, ракурсе, наклоне и наложении по отношению к наблюдателю, а не пространственные координаты того или иного объекта. Самое большое, на что они способны, – это объединить усилия, чтобы в результате получить 2,5-мерное представление о поверхностях перед нашими глазами, а перед мозгом стоит задача посложнее: выяснить, что делать с этой информацией дальше.