Свет, тень и форма

Стереоскопическое зрение – один из компонентов ключевого этапа зрительного восприятия, благодаря которому мозг определяет глубину и материал поверхности, но это не единственный его компонент. Чтобы видеть трехмерное изображение, не обязательно иметь два глаза. Достаточно полную информацию о форме и материале объекта можно извлечь даже из самых малозаметных особенностей изображения. Посмотрите на эти рисунки, которые придумал психолог Эдвард Адельсон[258].

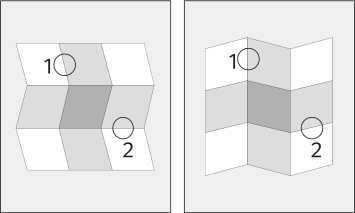
Кажется, что на рисунке слева – белый кусок картона с серой вертикальной полосой, сложенный по горизонтали и освещенный сверху, а справа – кусок белого картона с серой горизонтальной полосой, сложенный по вертикали и освещенный сбоку. (Если смотреть на рисунок достаточно долго, любой из этих рисунков может перевернуться в трехмерном пространстве, как куб Неккера, но пока нас интересует не это.) Вместе с тем, штрихи, из которых состоят оба рисунка на странице книги (и проекции на сетчатке ваших глаз), примерно одинаковы. Каждый рисунок представляет собой зигзагообразную фигуру из клеток, некоторые из которых затенены. На обоих рисунках угловые клетки белые, верхние и боковые клетки – светло-серые, а средняя клетка – более темного оттенка серого. Каким-то образом сочетание затенения и зигзагообразное™ заставляет рисунки приобретать объемность и интенсивность окраски, но по-разному. Границы, помеченные цифрой «1», физически являются идентичными на обоих рисунках. Тем не менее на левом рисунке эта граница выглядит как изображенная краской (как белая полоска, нарисованная рядом с серой полоской), а на правом рисунке – как граница, созданная изменением формы и затенения (светлая полоска, переходящая в тень на другой стороне сгиба). Границы, помеченные цифрой «2», также идентичны друг другу, и здесь наблюдателю тоже кажется, что они различаются, только наоборот: на левом рисунке тень, а на правом – полоска из краски. Все эти различия происходят лишь от того, что в одном случае сгиб сделан вовнутрь в том месте, где во втором случае сгиб сделан наружу! Чтобы увидеть так много в таком маленьком изображении, нужно раскрыть три закона, благодаря которым в мире существует изображение. Для каждого закона нам понадобится «эксперт» внутри нашего мышления. Как и в случае со стереозрением, работа этих экспертов позволяет нам получить точное представление о поверхностях объектов, однако для этого они используют другие типы информации, решают другие типы проблем и делают другие типы предположений о мире.

* * *

Первая проблема – это перспектива: проекция трехмерного объекта в виде двухмерного силуэта на сетчатке. К сожалению, любая проекция может получиться от бесконечного количества разных объектов, и способа восстановить форму объекта только по его проекции не существует (в этом могли убедиться посетители комнат Эймса). Создается такое впечатление, что эволюция говорит нам: «Ну что ж, никто не идеален», а наш анализатор формы заставляет нас видеть наиболее вероятное состояние окружающего мира, исходя из одного изображения на сетчатке.

Как система зрительного восприятия умудряется рассчитать наименее вероятное состояние мира, руководствуясь этим изображением? Теория вероятности предлагает простой ответ: теорема Байеса, самый незамысловатый способ определения вероятности гипотезы, основанной на каких-либо фактах. Согласно теореме Байеса, вероятность того, что одна гипотеза предпочтительнее другой, можно определить по двум показателям для каждой гипотезы. Один из них – априорная вероятность: какова ваша степень уверенности в этой гипотезе до того, как вы рассмотрите факты? Второй – это правдоподобие: если бы гипотеза была истинна, какова была бы вероятность возникновения фактов в том виде, в котором мы их наблюдаем? Умножаем априорную вероятность гипотезы 1 на вероятность возникновения фактов при условии истинности гипотезы 1. Умножаем вероятность гипотезы 2 на вероятность возникновения фактов при условии истинности гипотезы 2. Возьмем отношение этих двух чисел и получим перевес в пользу первой гипотезы.

Каким образом наш анализатор трехмерного изображения использует теорему Байеса? Он делает ставку на тот объект, который с наибольшей степенью вероятности мог бы дать такие линии, если бы присутствовал в этот момент в окружающей обстановке местности, и который с большой степенью вероятности встречается в типичной обстановке. Перефразируя слова Эйнштейна о Боге, можно сказать: анализатор формы исходит из предположения о том, что мир хрупок, но не зол[259].

Итак, в анализатор формы должна быть заложена информация об определенных вероятностных показателях, связанных с проекцией (о том, какими объекты кажутся в перспективе) и с окружающим миром (какие в нем бывают объекты). Некоторые из вероятностных характеристик, связанных с проекцией, играют очень большую роль. Теоретически монетка может давать проекцию в форме тонкой линии, но такое бывает, только если смотреть на нее со стороны ребра. Если в обстановке перед вашими глазами есть монетка, какова вероятность того, что вы смотрите на нее со стороны ребра? Если кто-нибудь специально не сделал так, чтобы эти два условия были одновременно выполнены, вероятность не очень велика. При наблюдении с многих других точек зрения проекция монетки будет иметь форму эллипса. Анализатор формы исходит из посылки о том, что заданная точка зрения – обобщенная (а не выверенная с прицельной точностью для желаемого расположения предметов, как в одной из комнат Эймса), и делает соответствующие ставки. С другой стороны, спичка почти всегда дает проекцию в форме прямой линии, так что если на изображении есть линия, то при прочих равных условиях спичка будет гораздо более вероятным предположением, чем монетка.

Если на изображении не одна, а несколько линий, то угадать становится еще проще. Так, совокупность параллельных или почти параллельных линий редко бывает случайной. Непараллельные линии в мире редко дают почти параллельные линии в проекции: если бросить на пол пару спичек, они в большинстве случаев лягут под тупым или острым углом по отношению друг к другу. В то же время линии, которые являются параллельными в реальном мире – например, края телеграфного столба – почти всегда дают проекцию в виде почти параллельных линий. Следовательно, если на изображении есть почти параллельные линии, велика вероятность того, что в реальном мире им соответствуют параллельные друг другу края объекта. Существует еще много практических способов указать, какие формы объектов реального мира могут с большой долей вероятности дать те или иные элементы изображения в проекции. Маленькие Т-образные, У-образные, V-образные элементы, углы, стрелочки, параллельные закорючки – это проекции самых разных прямых краев, углов и симметричных форм. Художники-карикатуристы веками использовали эти правила, а наш хитрый анализатор форм может использовать их в обратном порядке, делая ставки на то, какие объекты находятся перед нашими глазами.

Впрочем, естественно, использовать вероятность в обратном направлении – говорить, что параллельные линии всегда дают в проекции почти параллельное изображение, следовательно, почти параллельные линии в проекции всегда означают параллельные линии в реальном мире – ошибочно. Это все равно, что слышать топот копыт за окном и решить, что его производит зебра, поскольку зебра нередко бывает источником стука копыт. Нужно прежде всего учесть априорную вероятность того, что в мире есть данный объект. Как много вокруг нас зебр? Как много вокруг нас параллельных краев? Чтобы делающий ставки анализатор формы мог выполнять свою работу правильно, в мире должно быть множество прямых, ровных, симметричных и компактных объектов, которые ему так нравится угадывать. Но так ли это? Романтику может показаться, что природный мир органичен и мягок, что его резкие края словно сровняли с землей инженерные войска. Как недавно заявил своим студентам один профессор литературы, «Прямые линии добавлены в пейзаж человеком». Одна из студенток, Гейл Дженсен Сэнфорд, отнеслась к утверждению скептически и составила список прямых линий в природе, который недавно был опубликован в журнале «Харпере мэгэзин»:

Линия вдоль верхушки прибойной волны, горизонт в прериях, траектория падения капель во время сильного дождя или града, покрытые снегом поля, узоры кристаллов, линии белого кварца на поверхности гранита; сосульки, сталактиты, сталагмиты; поверхность спокойного озера; полоски на шкуре зебр и тигров; клюв утки; ноги кулика; клин перелетных птиц; бросок хищника; новый стебель папоротника; колючки кактуса; стволы молодых быстрорастущих деревьев; иголки сосны; нити паутины; трещины в поверхности льда; слои метаморфической горной породы; склоны вулкана; высококучевые облака, подгоняемые ветром; внутренняя поверхность месяца[260].

Некоторые из этих примеров спорны, другие вообще способны больше помешать анализатору формы, чем помочь. (Линия горизонта на озере или в прерии, а также край месяца вовсе не образованы линиями, которые мы видим в мире.) Тем не менее в целом подмечено верно. Законы, которым подчиняется физический мир, делают его состоящим из правильных, легко анализируемых форм. Движение, напряжение, притяжение образуют прямые линии. Сила притяжения действует под прямым углом. Сцепление дает ровные контуры. Движущиеся организмы, эволюционируя, приобретают симметрию. Естественный отбор преобразует части их тел в орудия труда, отвечая требованиям, аналогичным тем, что предъявляет инженер к хорошо обработанной детали. Большую поверхность образует множество элементов примерно одного размера и формы, расположенных примерно на одинаковом расстоянии: трещин, листьев, камешков, песчинок, небольших волн, иголок. И дело даже не в том, что те части реального мира, которые производят впечатление выструганных плотником и оклеенных обоями, проще всего распознать анализатору форм; просто именно такие его элементы стоят того, чтобы их распознать. Они представляют собой явные проявления мощных сил, которые наполняют и формируют нашу окружающую среду, и потому заслуживают большего внимания, чем обломки горных пород.

* * *

Даже самый лучший анализатор линий может справиться только с нарисованным миром. Поверхности не просто ограничены линиями; они состоят из материала. Наше ощущение света и цвета – это метод, с помощью которого мы проводим анализ материалов. Мы не кусаем пластмассовое яблоко, потому что его цвет подсказывает нам, что это не настоящий фрукт.

Анализ вещества на основе отражаемого им света – задача для эксперта по отражательной способности. Разные виды вещества отражают волны света разной длины и в разном количестве. (Чтобы было проще объяснить, я ограничусь только черным и белым; цвет делает ту же задачу примерно втрое сложнее.) К сожалению, данное количество отраженного света может происходить от бесконечного количества различных сочетаний вещества и освещения. Сто единиц силы света могут исходить как от угля, который отражает 10 % света 1000 свечей, так и от снега, отражающего 90 % света 111 свечи. Итак, нет надежного способа выяснить, из какого материала состоит объект, судя по отраженному им свету. Анализатор освещенности должен каким-то образом учесть коэффициент уровня освещенности. Это еще одна некорректно поставленная проблема, в точности похожая на следующую: я говорю число, а вы отвечаете, какие два числа я перемножил, чтобы его получить. Чтобы решить эту задачу, необходимо использовать дополнительные исходные посылки.

Перед фотоаппаратом стоит та же проблема: как сделать так, чтобы снежок всегда был белым, независимо от того, в доме он находится или на улице. Экспонометр фотоаппарата, измеряющий количество света, попавшего на пленку, является воплощением двух посылок. Первая – о том, что освещение единообразно: вся фотографируемая сцена находится либо на солнце, либо в тени, либо в условиях искусственного освещения. Нарушение этой посылки приводит к разочарованию для фотографа. Тетушка Мими становится грязно-серой фигурой на фоне синего неба, потому что фотоаппарат решил, что ее лицо находится в тени, а небо непосредственно освещено солнцем. Вторая посылка – о том, что сцена в среднем имеет средне-серый оттенок. Если взять некоторое количество случайным образом выбранных объектов, их разнообразие цвета и уровня освещенности будет в среднем представлять собой средне-серый оттенок, который отражает 18 % света. Фотоаппарат «предполагает», что перед ним – среднестатистическая картинка, и пропускает как раз столько света, чтобы средняя часть диапазона освещенности картинки в кадре получилась на пленке средне-серой. Участки более светлые, чем средняя часть диапазона, передаются с помощью светло-серого и белого; участки более темные – с помощью темно-серого и черного. Однако когда эта исходная посылка нарушается, и средним значением для картинки не оказывается серый цвет, фотоаппарат может обманываться. Кадр с черной кошкой на фоне черного бархата выходит средне-серым, кадр с белым медведем на фоне снега выходит средне-серым и т. д. Умелый фотограф анализирует то, насколько фотографируемая сцена отличается от среднестатистической, и компенсирует эту разницу, прибегая к различным уловкам. Примитивный, но достаточно эффективный прием – использовать карточку с образцом средне-серого цвета (который отражает ровно 18 % света), поднести ее к объекту и направить экспонометр на карточку. Теперь все соответствует исходной посылке об окружающем мире, которой руководствуется фотоаппарат, и его оценка уровня окружающего освещения (которая производится путем деления света, отраженного от карточки, на 18 %) будет верной[261].

Эдвин Лэнд, изобретатель поляризационного светофильтра и фотокамеры мгновенного действия «Полароид Лэнд», тоже столкнулся с этой проблемой, которая в цветной фотографии ощущается еще более остро. От электрической лампочки исходит оранжевый свет, от флуоресцентной лампочки – оливковый, от Солнца – желтый, от неба – голубой. Наш мозг каким-то образом выносит за скобки цвет освещения – точно так же, как он выносит за скобки интенсивность освещения – и видит объект при этом освещении в правильном цвете. Фотоаппарат на это не способен. Если только он не добавит к обстановке собственный элемент освещения – белую вспышку, то кадр, сделанный внутри помещения, получится с оттенком ржавчины, кадр, сделанный в тени – нездорового синеватого цвета и т. д. Опытный фотограф, чтобы компенсировать этот эффект, приобретет специальную пленку или накрутит на объектив фильтр, хороший лаборант-оператор может подправить цвет перед печатью фотографии, а вот фотокамера мгновенного действия на это явно не способна. Поэтому Лэнд был с практической точки зрения заинтересован в том, чтобы найти способ избавиться от интенсивности и цвета освещения (эта проблема известна как константность цвета).

В то же время Лэнд был гениальным исследователем восприятия, хотя и самоучкой, и заинтересовался тем, как с этой задачей справляется мозг. Он создал лабораторию восприятия цвета и разработал блестящую теорию константности цвета. Его идея, получившая название ретинальной теории, подразумевала, что восприятие основано на нескольких исходных посылках. Первая посылка – о том, что земное освещение – это насыщенная смесь волн разной длины. (Исключение, которое подтверждает правило – натриевая лампа, энергосберегающее устройство, которое можно увидеть на парковках. Эта лампа испускает волны узкого диапазона частот, которые наша система восприятия не способна вынести за скобки; машины и лица под таким освещением приобретают мертвенно-бледный желтый оттенок.) Вторая посылка состоит в том, что неравномерность яркости и цветности в пределах поля зрения, вероятно, связана с тем, как освещена сцена, в то время как резкие переходы соответствуют границе, где заканчивается один объект и начинается другой. Чтобы не усложнять эксперимент, Лэнд тестировал свою модель на искусственных моделях мира, состоящих из двухмерных квадратных кусочков; он назвал их «мондрианами» в честь голландского художника. Если такой мондриан осветить сбоку, то желтый участок с одной его стороны отражает совсем не такой свет, как точно такой же желтый участок с другой стороны. Тем не менее людям оба эти кусочка кажутся желтыми – и точно так же их воспринимает ретинекс, устраняющий неравномерность освещения от одного края до другого[262].

Ретинальная теория была хорошим началом, но в итоге оказалось, что она все упрощает. Одна из проблем заключалась в предположении, что мир – это мондриан, то есть большая плоскость. Но вернемся к рисункам Адельсона на странице 242, которые представляют собой зигзагообразные мондрианы. Ретинекс воспринимает все резкие границы одинаково, и границу № 1 на левом рисунке он интерпретирует точно так же, как границу № 2 на правом рисунке. Тем не менее для нас левая граница выглядит как граница между полосками двух разных цветов, а правая – как единая полоска, которая сложена пополам и находится частично в тени. Это различие обусловлено нашей способностью интерпретировать трехмерные формы. Анализатор формы увидел в этих мондрианах полосатые ширмы, а ретинекс видит в них все туже самую шахматную доску. Очевидно, что ему чего-то не хватает.

* * *

Это что-то – влияние, которое ракурс оказывает на затенение, третий закон, который превращает зрительную сцену в изображение. Поверхность, обращенная к источнику света фронтально, отражает большое количество света, потому что свет врезается в поверхность и отскакивает от нее. Поверхность, помещенная под углом почти параллельно источнику света, отражает намного меньше света, потому что он по большей части падает на нее под скользящим углом и проходит дальше. Если наблюдатель стоит рядом с источником света, то глаз улавливает больше света, когда поверхность расположена фронтально, чем когда она расположена почти боком. Это различие можно увидеть, если посветить фонариком на кусок серого картона, одновременно вращая картон вокруг своей оси.

Как же может наш анализатор затенения использовать этот закон в обратном направлении и определить ракурс поверхности исходя из того, как много света она отражает? Преимущества этой способности не ограничиваются только тем, что мы можем оценить ракурс плоской поверхности. Многие объекты (например, кубики и драгоценные камни) состоят из граней, расположенных под углом друг к другу, и определение угла уклона необходимо для того, чтобы установить их форму. На самом деле, любую форму можно представить как высеченную фигуру, состоящую из миллионов крошечных граней. Даже если поверхность составляют настолько сглаженные кривые, что размер каждой «грани» сводится к точке, закон затенения все равно применим к свету, отражающемуся от каждой из этих точек. Если бы закон можно было использовать в обратном направлении, наш анализатор затенения мог бы оценить форму поверхности и зарегистрировать угол уклона касательной плоскости к поверхности в каждой из точек.

К сожалению, данное количество света, отраженное от участка поверхности, может происходить как от темной поверхности, расположенной под углом к источнику света, так и от светлой поверхности, расположенной под углом от источника света. Следовательно, нет надежного способа установить ракурс поверхности по количеству отраженного ею света без дополнительных исходных посылок.

Первая посылка заключается в том, что освещение поверхности равномерно: что весь мир сделан из гипса. Когда поверхность окрашена неравномерно, эта посылка нарушается, и наш анализатор затенения может быть введен в заблуждение. Так и происходит. Наиболее очевидный пример – это картины и фотографии. Менее очевидный – это защитная окраска по принципу противотени у животных. Узор на шерсти многих животных в направлении от спины к животу образует постепенный переход от темного к светлому, который компенсирует трехмерность их формы, создаваемую освещением. Это делает животное зрительно плоским, благодаря чему анализатору в мозге хищника, делающему предположения о форме на основе затенения, становится сложнее его обнаружить. Еще один пример – макияж. Если макияжа на лице не так много, как у Тэмми Фэй Беккер, то краска, нанесенная на кожу, вполне может заставить наблюдателя думать, что плоть и кости под этой кожей имеют более идеальную форму. Темные румяна, нанесенные на крылья носа, создают впечатление, что они расположены под меньшим углом к источнику света, отчего нос кажется более тонким. Светлая пудра, нанесенная на верхнюю губу, работает прямо противоположным образом: получается впечатление, что свет падает на губу фронтально, как если бы она была более объемной, что создает столь желанный эффект пухлых губ.

Анализатору, определяющему форму по степени затенения, тоже не обойтись без дополнительных исходных посылок. Поверхности объектов в окружающем мире состоят из тысяч разных материалов, и свет отражается от их плоскостей, расположенных под разными углами, очень по-разному. Матовая поверхность наподобие мела или матовой бумаги отражает свет в соответствии с простым законом, и наш анализатор затенения часто исходит из предположения, что весь мир – матовый. Поверхности, на которых имеется блеск, налет, пушок, углубления, выпуклости, совсем иным, более необычным образом реагируют на освещение и потому могут ввести глаза в заблуждение[263].

Широко известный пример – полная Луна. Она выглядит как плоский диск, хотя, конечно же, на самом деле представляет собой шар. Мы без проблем определяем форму всех остальных сфер – например, мячика для пинг-понга – по затенению, и любой хороший художник может сделать набросок шара карандашом. Проблема с Луной в том, что ее поверхность испещрена кратерами разных размеров; большинство из них слишком малы, чтобы их можно было различить с Земли, поэтому в сочетании они образуют поверхность, которая ведет себя совершенно не так, как матовая идеальная поверхность, которую принимает за данность наш анализатор затенения. Центр полной Луны обращен к наблюдателю фронтально, следовательно, он должен быть самой яркой ее точкой, однако и в центре есть маленькие углубления и трещинки, стенки которых обращены к наблюдателю, стоящему на Земле, ребром, в результате чего центральная часть Луны кажется темнее. Поверхности ближе к периметру Луны находятся на касательной прямой к линии взора и вроде бы должны казаться темнее, однако стенки расположенных здесь ущелий и кратеров повернуты к наблюдателю фронтально и отражают большое количество света, из-за чего периметр Луны выглядит светлее. Если мы возьмем диск Луны в целом, угол ее поверхности и угол, под которым расположены стенки кратеров, компенсируют друг друга; все участки лунной поверхности отражают одинаковое количество света, и глаз видит ее как диск[264].

* * *

Если бы мы полагались только на один из перечисленных анализаторов, мы бы срывали с деревьев кору вместо плодов и падали с обрывов. Каждый анализатор исходит из своих посылок, однако этим посылкам нередко противоречат посылки других анализаторов. Ракурс, форма, материал, освещение – все эти параметры тесно связаны, а нам нужно как-то распутать этот клубок и увидеть одну форму одного цвета, расположенную под одним углом и при одном освещении. Как же нам это удается?

Адельсон в соавторстве с психологом Алексом Пентландом придумал для своей иллюзии с зигзагами небольшую аллегорию. Вы – дизайнер, который должен создать декорации, выглядящие в точности как схема справа. Вы идете в мастерскую, где работают несколько специалистов, занимающиеся изготовлением декораций для театральных постановок. Один – художник. Второй – художник-осветитель. Третий – жестянщик. Вы показываете им картинку и просите сделать декорации, которые будут выглядеть точно так же. В сущности, они должны сделать то, что делает зрительная система: на основе изображения определить расположение реальных объектов и освещение, которое могло бы дать такое изображение.

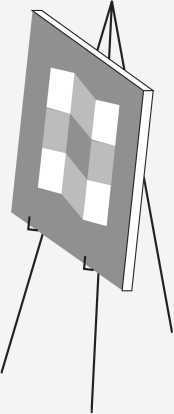
Есть много способов, которыми мастера могут выполнить поставленную задачу. Каждый из них может справиться практически без помощи остальных. Художник может просто нарисовать композицию из параллелограммов на плоском листе металла и попросить художника-осветителя осветить ее одним прожектором:

Художник-осветитель может взять простой лист белой бумаги и установить девять светильников направленного света, каждый из которых будет оснащен специальным фильтром и теневой маской, и направить их таким образом, чтобы на листе получились девять параллелограммов (шесть из этих прожекторов показаны на рисунке на с. 278):

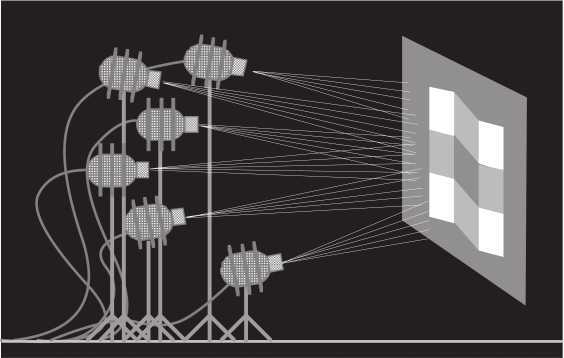
Жестянщик может изготовить из листов металла такие формы, которые при нужном освещении и наблюдении с определенной точки давали бы такое изображение:

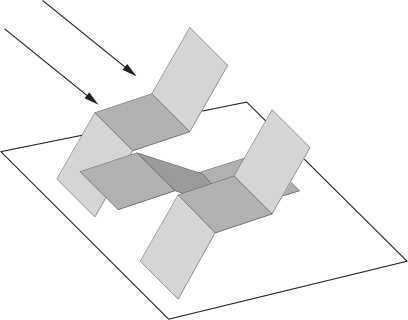
Наконец, мастера могут создать такое изображение и путем совместной работы. Художник нарисует полоску посередине квадратного листа металла, жестянщик согнет его зигзагообразно, а художник-осветитель осветит его прожектором. Конечно, именно так действует мозг человека, чтобы интерпретировать изображение.

Перед нашим мозгом стоит такой же сложный выбор, как перед дизайнером в этой притче. Если мы допустим к работе ментального эксперта, формулирующего предположения о существовании окрашенных поверхностей, он может интерпретировать все особенности изображения как особенности нанесения краски: весь мир для него будет мастерски выполненной оптической иллюзией. Аналогичным образом специалист по освещению в нашей голове мог бы сказать, что весь мир – это кино. Поскольку такая интерпретация мира нежелательна, нужно каким-то образом не допустить, чтобы наши ментальные эксперты сделали подобные выводы. Один способ добиться этого – заставить их действовать в соответствии с исходными посылками, несмотря ни на что (цвет и освещение равномерны, формы правильны и параллельны), однако этот способ слишком радикален. Мир не всегда представляет собой кучу кирпичей в солнечный день. Иногда в нем встречается сложное освещение и окраска, и мы все равно их видим. Нам не нужно, чтобы эксперты отрицали сложность мира. Нам нужно, чтобы они предполагали существование в мире ровно такой степени сложности, как это есть на самом деле, и ничуть не больше. Проблема в том, как заставить их сделать это.

Вернемся к нашей притче. Предположим, что у отдела декораций ограниченный бюджет. Все специалисты назначают за свои услуги плату в соответствии с прейскурантом, который отражает сложность и нестандартность оказываемой услуги. Простые и стандартные операции стоят недорого; сложные и необычные операции дороже.

Нам нужен еще один специалист: руководитель, который решает, как распределить работу.

Для всех четырех решений стоимость работ будет разной. Вот смета стоимости:

Решение с руководителем – наименее затратное, потому что в этом случае услуги каждого специалиста используются оптимально и сэкономленных денег оказывается более чем достаточно, чтобы оплатить услуги руководителя. Мораль в том, что работой специалистов нужно руководить, и делать это должен не обязательно гомункул или демон, а некая схема, позволяющая минимизировать затраты, при которой «дешево» будет означать «просто», а «просто» будет означать «вероятно». Из нашей притчи видно, что простые операции легче выполнить; в случае со зрительной системой это означает, что простые описания соответствуют более вероятной конфигурации объектов в реальном мире.

Адельсон и Пентланд воплотили свою аллегорию в жизнь, создав на компьютере модель зрительной системы, задача которой – интерпретировать сцены с нарисованными многоугольниками так, как это делает человек. Первым делом анализатор формы (который в программе выполняет роль жестянщика) ищет самую правильную форму, соответствующую изображению. Возьмем простую фигуру, изображенную на схеме ниже слева: люди видят ее как сложенный лист, наподобие развернутой книги.

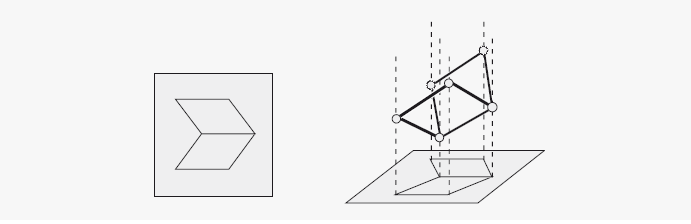
Специалист – анализатор форм – пытается собрать трехмерную модель из полученного на входе изображения, показанного справа. В самом начале ему известно только то, что углы и края модели должны быть выровнены с точками и линиями на изображении; ему неизвестно, на какой глубине они находятся. Вершины модели – это шарики на штангах (как линии проекции), а соединяющие их линии – бесконечно эластичные струны. Специалист передвигает шарики по струнам, пока не получит форму, соответствующую следующим требованиям. Каждый многоугольник, составляющий фигуру, должен быть по возможности правильным; то есть его углы должны не очень сильно различаться. Например, если у многоугольника четыре стороны, специалист старается создать прямоугольник. Многоугольник должен по возможности лежать в одной плоскости, как если бы он представлял собой лист пластмассы, который сложно согнуть. Наконец, многоугольник должен быть как можно более компактным, а не вытянутым относительно линии взора – как если бы этот лист пластмассы было сложно растянуть.

Когда специалист по определению формы заканчивает свою работу, он передает жесткую конструкцию из белых листов специалисту по освещению. Специалист по освещению знает законы, которые определяют, каким образом отраженный свет зависит от освещения, от степени освещенности поверхности и от угла расположения поверхности. Специалисту дается возможность перемещать единственный источник дальнего света таким образом, чтобы освещать модель с разных направлений. Оптимальным направлением будет такое, при котором каждая пара листов, соединенных ребром, будет выглядеть максимально похоже на соответствующие поверхности изображения, чтобы для завершения работы потребовалось как можно меньше серой краски.

Наконец, модель попадает в руки специалиста по отражательной способности – художника. Этот специалист – последняя инстанция, и его задача – устранить любое остающееся несоответствие между изображением и моделью. В завершение работы он предлагает разные оттенки цвета различных поверхностей.

Работает ли эта программа? Адельсон и Пентленд поставили перед ней объект в форме гармошки и дали ей возможность импортировать образ. Программа отображает текущие предположения о форме объекта (первая колонка), текущие предположения о направлении источника света (вторая колонка), текущие предположения относительно того, куда падает тень (третья колонка), и текущие предположения о том, как объект окрашен (четвертая колонка). Первые предположения программы приведены в верхнем ряду.

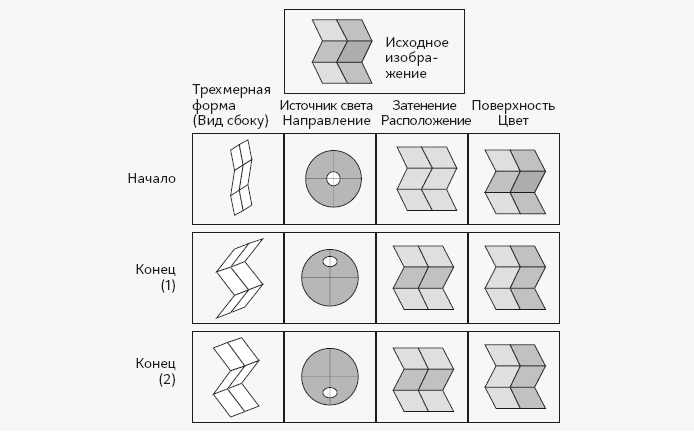
Изначально программа предположила, что объект плоский, как двухмерная картина, лежащая на столе, как видно из верхней строки в первой колонке. (Вам сложно это представить, потому что ваш мозг упорно продолжает видеть зигзагообразную форму как полоску, изогнутую в пространстве. На этом рисунке предпринята попытка показать некоторые линии как располагающиеся на странице в плоскости.) Программа предположила, что источник света направлен фронтально, в направлении от положения глаза (верхний ряд, второй столбец). При таком плоском освещении теней почти не получается (верхний ряд, третья колонка). Специалист по отражательной способности несет ответственность за удваивание изображения и просто дорисовывает его. Программа думает, что перед ней – картинка.

Как только программа получает возможность поправить свои предположения, у нее получается интерпретация, представленная в среднем ряду. Специалист по форме находит самую правильную трехмерную форму (в левом столбце показан ее вид сбоку), состоящую из квадратных листов, соединенных под нужными углами. Специалист по освещению обнаруживает, что, направив свет сверху, он может получить игру теней, которая будет напоминать исходное изображение. Наконец, специалист по отражательной способности наносит на модель краску. Четыре столбца – зигзагообразная трехмерная фигура, свет, направленный сверху, тени в середине фигуры, полоска света рядом с темной полоской – соответствуют тому, как люди интерпретируют исходное изображение[265].

Напоминает ли эта программа человека еще чем-нибудь? Вспомним, как сложенная гармошкой фигура переворачивается в пространстве подобно кубу Неккера. Внешний сгиб становится внутренним и наоборот. Программа тоже в определенном смысле способна увидеть этот переворот; «перевернутая» интерпретация показана в нижнем ряду. Программа считает, что издержки на получение обеих интерпретаций будут одинаковы, и делает выбор в пользу первой или второй наугад. Когда люди видят переворот фигуры в пространстве, они обычно видят и переворот направления источника света: верхний сгиб наружу, освещение направлено сверху; нижний сгиб наружу, освещение направлено снизу[266]. Программа делает то же самое. На самом деле, в отличие от человека, программа не «перескакивает» от одной интерпретации к другой, но если бы «специалисты» Адельсона и Пентланда работали не по образцу конвейера, а в условиях сети ограничений (наподобие сети на с. 124, работающей с кубом Неккера, или модели стереозрения), это было бы возможно.

Аллегория с мастерской наглядно подтверждает идею о том, что разум – это совокупность модулей, система органов или сообщество экспертов. Эксперты нужны постольку, поскольку нужно экспертное мнение: проблемы, с которыми сталкивается мышление, слишком узкоспециальны, чтобы их мог решить мастер на все руки. По большей части информация, которая нужна одному из экспертов, не имеет значения для другого и даже мешает ему в работе. С другой стороны, работая изолированно, эксперт может рассмотреть слишком много решений или упорно цепляться за единственное решение; в какой-то момент экспертам бывает нужно посовещаться. Все эти многочисленные эксперты вместе пытаются разобраться в одном мире, и этот мир безразличен к их попыткам: он не предлагает легких решений, но и не делает все возможное, чтобы сбить их с толку. Поэтому схема работы с участием руководителя направлена на то, чтобы эксперты уложились в бюджет, учитывая, что маловероятные предположения обходятся дороже. Это заставляет их сообща делать наиболее вероятные в целом предположения относительно того, что происходит в окружающем мире.